Columnar Transposition Cipher
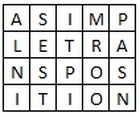
Columnar Transposition involves writing the plaintext out in rows, and then reading the ciphertext off in columns. In its simplest form, it is the Route Cipher where the route is to read down each column in order. For example, the plaintext "a simple transposition" with 5 columns looks like the grid below
So far this is no different to a specific route cipher. Columnar Transposition builds in a keyword to order the way we read the columns, as well as to ascertain how many columns to use.
Encryption
We first pick a keyword for our encryption. We write the plaintext out in a grid where the number of columns is the number of letters in the keyword. We then title each column with the respective letter from the keyword. We take the letters in the keyword in alphabetical order, and read down the columns in this order. If a letter is repeated, we do the one that appears first, then the next and so on.
We first pick a keyword for our encryption. We write the plaintext out in a grid where the number of columns is the number of letters in the keyword. We then title each column with the respective letter from the keyword. We take the letters in the keyword in alphabetical order, and read down the columns in this order. If a letter is repeated, we do the one that appears first, then the next and so on.
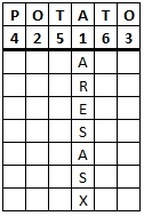
As an example, let's encrypt the message "The tomato is a plant in the nightshade family" using the keyword tomato. We get the grid given below.
|
We have written the keyword above the grid of the plaintext, and also the numbers telling us which order to read the columns in. Notice that the first "O" is 3 and the second "O" is 4, and the same thing for the two "T"s.
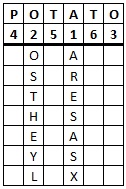
|
Starting with the column headed by "A", our ciphertext begins "TINESAX" from this column. We now move to the column headed by "M", and so on through the letters of the keyword in alphabetical order to get the ciphertext "TINESAX / EOAHTFX / HTLTHEY / MAIIAIX / TAPNGDL / OSTNHMX" (where the / tells you where a new column starts). The final ciphertext is thus "TINES AXEOA HTFXH TLTHE YMAII AIXTA PNGDL OSTNH MX".
Decryption
The decryption process is significantly easier if nulls have been used to pad out the message in the encryption process. Below we shall talk about how to go about decrypting a message in both scenarios.
The decryption process is significantly easier if nulls have been used to pad out the message in the encryption process. Below we shall talk about how to go about decrypting a message in both scenarios.
Firstly, if nulls have been used, then you start by writing out the keyword and the alphabetical order of the letters of the keyword. You must then divide the length of the ciphertext by the length of the keyword. The answer to this is the number of rows you need to add to the grid. You then write the ciphertext down the first column until you reach the last row. The next letter becomes the first letter in the second column (by the alphabetical order of the keyword), and so on.
As an example, we shall decrypt the ciphertext "ARESA SXOST HEYLO IIAIE XPENG DLLTA HTFAX TENHM WX" given the keyword potato. We start by writing out the keyword and the order of the letters. There are 42 letters in the ciphertext, and the keyword has six letters, so we need 42 ÷ 6 = 7 rows.
Now we read off the plaintext row at a time to get "potatoes are in the nightshade family as well".
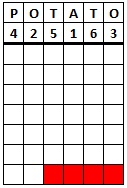
When no nulls have been used we have to do a slightly different calculation. We divide the length of the ciphertext by the length of the keyword, but this is likely to not be a whole number. If this is the case, then we round the answer up to the next whole number. We then multiply this number by the length of the keyword, to find out how many boxes there are in total in the grid. Finally, we take the length of the ciphertext away from this answer. Thie number (which should be less than the length of the key) is how many nulls there would have been if used, so we need to black out these last few boxes, so we don't put letters in them whilst decrypting.
To decrypt the ciphertext "ARESA SOSTH EYLOI IAIEP ENGDL LTAHT FATEN HMW", we start similarly to above, by heading the columns with the keyword potato. This time, to find how many rows we need, we do 38 ÷ 6 = 6.3333. We round this up to the next number, which is 7, so we need 7 rows. Whe we multiply 6 x 7 we get 42, and 42 - 38 = 4. Hence we need 4 placeholders in the last row. We get the grid below to the left. After pluggin the ciphertext letters in, in the same way as above, we get the grid on the right.
Finally, we read off the plaintext in rows, to reveal the same plaintext as the other example, "potatoes are in the nightshade family as well".
Discussion
Columnar Transposition has the security of a transposition cipher with the extra befefit of utilizing a keyword. This is easier to remember than some complex route, and provides a better mixing effect than the railfence cipher.
Columnar Transposition has the security of a transposition cipher with the extra befefit of utilizing a keyword. This is easier to remember than some complex route, and provides a better mixing effect than the railfence cipher.
One of the key benefits of a transposition cipher over a substitution cipher is that they can be applied more than once. For example, the Columnar Transposition cipher could be applied twice on the plaintext. This is done by following the process above to produce some ciphertext, but then to use the same (or a different) keyword and to plug this ciphertext into the grid and read off the rows again. Our example above would give us
After this double transposition, we get the ciphertext "EATMX DHNOH YIGNI EXEAN TATTI AOXTX FHIPS SHLAT LM".
This double transposition increases the security of the cipher significantly. It could also be implemented with a different keyword for the second iteration of the cipher. In fact, until the invention of the VIC Cipher, Double Transposition was seen as the most secure cipher for a field agent to use reliably under difficult circumstances.