Fractionating Ciphers
Fractionation is a method of splitting letters so that each plaintext letter is represented by two or more symbols. This is different to Homophonic Substitution in that the same set of symbols are used to represent each plaintext letter each time, it is just there is more than one symbol. For example, "a" could be represented by "01", "b" by "02" and so on. Carrying this on we would get the ciphertext alphabet below.
The ciphertext alphabet when each plaintext letter is represented by two digits.
We can now encrypt a plaintext message "flee at once". We get "06120505 0120 15140305" as our ciphertext. Clearly this is a simple key, and we can use a more complex ciphertext alphabet. This makes the message harder to break, however, we have still only used a simple Monoalphabetic Substitution at this point. It is still susceptible to frequency analysis, but rather than looking at individual digits, we look at pairs (or digraphs). In our ciphertext, the most frequent digraph is "05" which appears 3 times, and does indeed represent "e".
So fractionation has made our substitution a little bit more secure, but it is still vulnerable (and at this stage most definitely less secure than the Polyalphabetic Ciphers).
However, fractionation is a useful tool to help make other ciphers (namely Transposition Ciphers) much more secure. We already looked at combining a monoalphabetic substitution with a transposition cipher, and when we use a fractionating method in our substitution it turns out to be even more secure.
As a simple example, we could reverse the words, giving us the new ciphertext "50502160 0210 50304151". This is still susceptible to frequency analysis, but the words would be reverted, which makes it a little harder to spot the patterns.
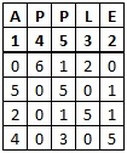
Now let's try a Columnar Transposition on the original ciphertext using keyword apple. We get the grid below.
The columnar transposition grid on the original ciphertext.
|
From this we read off our new ciphertext "05240115205060001513".
|
Now if we try to decipher this message with the ciphertext alphabet above, we start fine until we get to "50" and "60" which are not available. This method has turned a plaintext of 10 letters into a ciphertext of 20 digits, which we have jumbled up so it cannot be undone without the transposition first.
This is the power of a fractionating method. It allows us to not only pull apart words (like a normal transposition) but actually pull apart the individual letters of a message! It also allows us to represent a set of letters with a smaller set of characters (in this case the 26 letters are represented by 10 digits).
In this section we will look at two methods of fractionating a plaintext: We will then look at how we can combine these fractionating methods with a Transposition Cipher to make them even more secure.
And finally another way to alter the fractionated text in a way to make it harder to break.
And finally another way to alter the fractionated text in a way to make it harder to break.