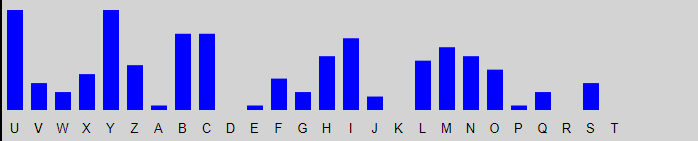Kasiski Analysis: Breaking the Code
The strength of the Vigenère Cipher is that it is not susceptible to Frequency Analysis, due to the fact that the cipher rotates through different shifts, so the same plaintext letter will not always be encrypted to the same ciphertext letter. For example, if "P" is the most common letter in the ciphertext, we might assume this is "e". However, with the Vigenère Cipher this is not the case.
For many centuries the Vigenère cipher was thought to be unbreakable, although Charles Babbage is known to have broken certain variants of it as early as 1854, though he did not publish his work. However it was Friedrich Kasiski who published a complete account of how to break the Vigenère Cipher in 1863, which did not rely on any knowledge of either the plaintext or the key.
Here we shall discuss how the Kasiski Examination works, after which we shall go through an extended example of how to use the activity to help break a message encoded using the Vigenère Cipher.
The Method
Although we have flattened out the frequency of the letters in the ciphertext by using a different shift for each letter, there is one main weakness to the security of the Vigenère Cipher. And that is the fact that the key is repeated.
Although we have flattened out the frequency of the letters in the ciphertext by using a different shift for each letter, there is one main weakness to the security of the Vigenère Cipher. And that is the fact that the key is repeated.
If we use the keyword key, then the keystream will be keykeykeykeykey... This means that every third letter is encrypted using the same shift. Essentially, we have 3 interwoven Caesar Ciphers, which can each individually be broken by frequency analysis. The hard part is thus working out the length of the keyword.
The solution that Kasiski came up with was ingenious. As an example, consider what we get when we encode the plaintext "maths is short for mathematics" using the keyword key we get the ciphertext shown in the table below. The important things to notice are the two bits that are bolded. Due to the repeating nature of the key, both times we see "math", it is encrypted in the same way to "WERR".
Encoding using the keyword key. Notice the repetitions in bold
As a cryptanalyst this gives us some useful information. Since the repeating are 15 letters apart, we know that the length of the key must be a factor of 15. That is, the key must repeat exactly in a space of 15 letters. So the keyword must be one of the lengths 15, 5, 3 or 1. Now it can't be one (then it would be a simple Caesar Shift), and it is unlikely to be of length 15, so now we could analyse each of the instances of keywords of length 3 and 5.
This is a good first step, however it is possible that repeating strings of letters in the ciphertext could be coincidence, so we want to have more information. If we look at the intercepted message below then we can see two sets of repeating strings.
VHVSSPQUCEMRVBVBBBVHVSURQGIBDUGRNICJQUCERVUAXSSR
Following a similar approach to before, the gap between the "VHVS" pair is 18, suggesting a key length of 18, 9, 6, 3 or 2. The gap between the "QUCE" pair is 30, which suggests a key length of 30, 15, 10, 6, 5, 3 or 2. So looking at both together the most likely key length is 6 or possibly 3 (though in practice this is unlikely).
This method can be extended to look for many trigraphs and higher n-graphs, and by taking the factor that appears the most commonly, you can ascertain with confidence the length of the keyword. Obviously, the longer the message the more repeated n-graphs there are likely to be, and the more confident you can be about the length of the keyword.
Once you know the length of the keyword, you can write out the ciphertext is that many columns. For example, if the keyword is 6 letters long, write the ciphertext in 6 columns. Now the letters in each column have all been encoded using the same keyword letter, and thus the same shift. So a bit of frequency analysis will help us with each individual column.
Worked example
In this example we shall use Kasiski Analysis to break the code used to encrypt the intercept given below, given that it has been encrypted with a Vigenère Cipher.
In this example we shall use Kasiski Analysis to break the code used to encrypt the intercept given below, given that it has been encrypted with a Vigenère Cipher.
|
CVJTNAFENMCDMKBXFSTKLHGSOJWHOFUISFYFBEXEINFIMAYSSDYYIJNPWTOKFRHWVWTZFXHLUYUMSGVDURBWBIVXFAFMYFYXPIGBHWIFHHOJBEXAUNFIYLJWDKNHGAOVBHHGVINAULZFOFUQCVFBYNFTYGMMSVGXCFZFOKQATUIFUFERQTEWZFOKMWOJYLNZBKSHOEBPNAYTFKNXLBVUAXCXUYYKYTFRHRCFUYCLUKTVGUFQBESWYSSWLBYFEFZVUWTRLLNGIZGBMSZKBTNTSLNNMDPMYMIUBVMTLOBJHHFWTJNAUFIZMBZLIVHMBSUWLBYFEUYFUFENBRVJVKOLLGTVUZUAOJNVUWTRLMBATZMFSSOJQXLFPKNAULJCIOYVDRYLUJMVMLVMUKBTNAMFPXXJPDYFIJFYUWSGVIUMBWSTUXMSSNYKYDJMCGASOUXBYSMCMEUNFJNAUFUYUMWSFJUKQWSVXXUVUFFBPWBCFYLWFDYGUKDRYLUJMFPXXEFZQXYHGFLACEBJBXQSTWIKNMORNXCJFAIBWWBKCMUKIVQTMNBCCTHLJYIGIMSYCFVMURMAYOBJUFVAUZINMATCYPBANKBXLWJJNXUJTWIKBATCIOYBPPZHLZJJZHLLVEYAIFPLLYIJIZMOUDPLLTHVEVUMBXPIBBMSNSCMCGONBHCKIVLXMGCRMXNZBKQHODESYTVGOUGTHAGRHRMHFREYIJIZGAUNFZIYZWOUYWQZPZMAYJFJIKOVFKBTNOPLFWHGUSYTLGNRHBZSOPMIYSLWIKBANYUOYAPWZXHVFUQAIATYYKYKPMCEYLIRNPCDMEIMFGWVBBMUPLHMLQJWUGSKQVUDZGSYCFBSWVCHZXFEXXXAQROLYXPIUKYHMPNAYFOFHXBSWVCHZXFEXXXAIRPXXGOVHHGGSVNHWSFJUKNZBESHOKIRFEXGUFVKOLVJNAYIVVMMCGOFZACKEVUMBATVHKIDMVXBHLIVWTJAUFFACKHCIKSFPKYQNWOLUMYVXYYKYAOYYPUKXFLMBQOFLACKPWZXHUFJYGZGSTYWZGSNBBWZIVMNZXFIYWXWBKBAYJFTIFYKIZMUIVZDINLFFUVRGSSBUGNGOPQAILIFOZBZFYUWHGIRHWCFIZMWYSUYMAUDMIYVYAWVNAYTFEYYCLPWBBMVZZHZUHMRWXCFUYYVIENFHPYSMKBTMOIZWAIXZFOLBSMCHHNOJKBMBATZXXJSSKNAULBJCLFWXDSUYKUCIOYJGFLMBWHFIWIXSFGXCZBMYMBWTRGXXSHXYKZGSDSLYDGNBXHAUJBTFDQCYTMWNPWHOFUISMIFFVXFSVFRNA
|
The first step is to find as many sets of repeating n-graphs as we can, and the distance between each of them. This is a very long-winded process to undertake by hand. Fortunately, computers have made searches like this possible in a matter of seconds. Copy the text above, and paste it into the activity at the top of the page. Now click "Find Repeated Sequences".
The start of the output from the Kasiski Analysis activity
The activity creates a list of all the sets of repeating 4-graphs and 3-graphs. For each of these, it finds the distance between the two repeating units (the number given next to the repeating unit), and then highlights all the factors (below 25) of this distance. So the two appearances of "ZFOK" are 18 letters apart, suggesting a keyword of length 18, 9, 6, 3 or 2. When we look down the whole set of repeating units we are looking for the highest number that is selected in most of the pairs of repeating units. In this case the most likely key length is 6. Notice that 2 and 3 are also very highly appearing. If the key was of length 3, you would not expect so many 6's to be highlighted.
It does not hae to be every single repeating unit, but there should only be very few that do not work. Below is shown one that has a strange repetition compared to the rest of the units, and this is purely a coincidental repitition. This is why we must check many units, as this one seen alone would be very misleading.
Notice that this trigraph has a strange repetitive nature
|
Now that we are pretty sure that the keyword has a length of 6 letters, we can analyse each set of ciphertext letters that was encoded by the same keyword letter. If looking at this by hand, the easiest way to do this is to write the intercept out in 6 columns, each headed by a letter of the keyword.
|
Splitting the ciphertext into columns
|
Choose the number of letters you think are in the keyword
|
In the activity, you now use the stepper to choose how many letters you think there are in the keyword. As you add letters, the list to the right will populate with the correct number of letters, labelled as "L1", "L2", etc up to "L6" in this case.
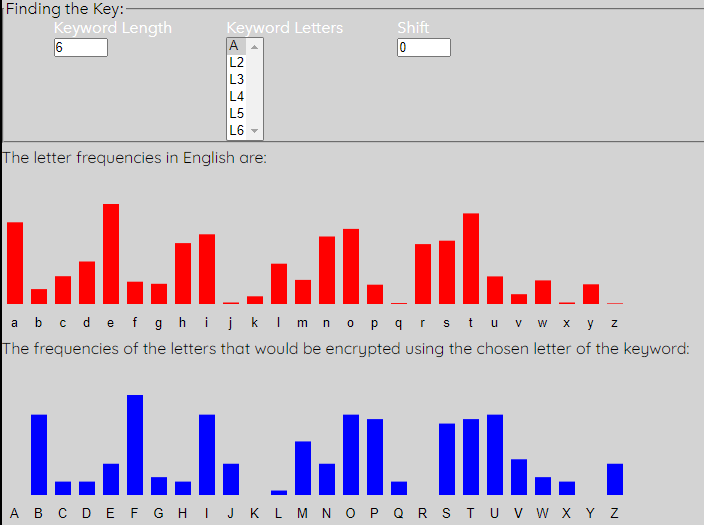
We are now going to perform frequency analysis on each of the sets of letters that correspond to each letter of the keyword (ie look at each column of letters). To do this, click on "L1".
|
The output when we perform frequency analysis on the first column of letters from the intercept
Notice that the "L1" has now become "A", and that every letter that corresponds to this keyword letter (ie would be in the first column) has been converted in the "Decrypted Message" box.
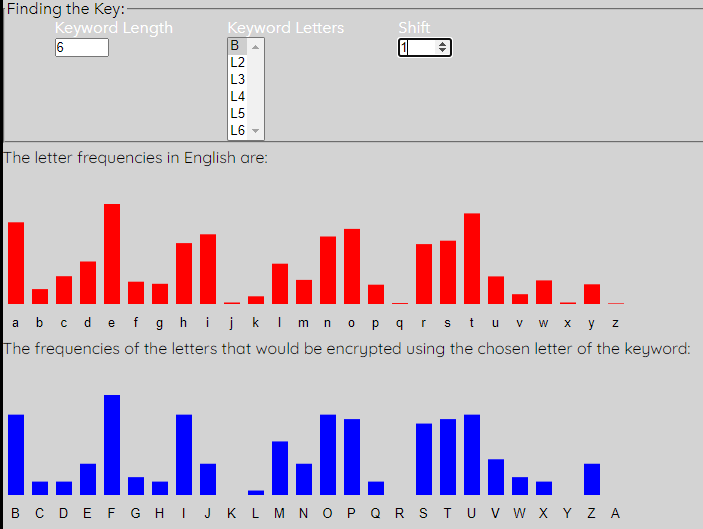
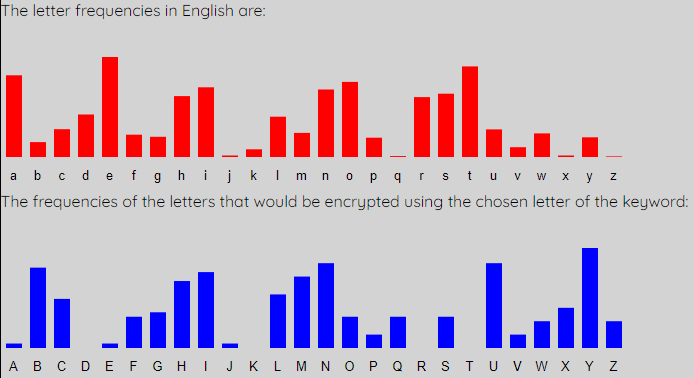
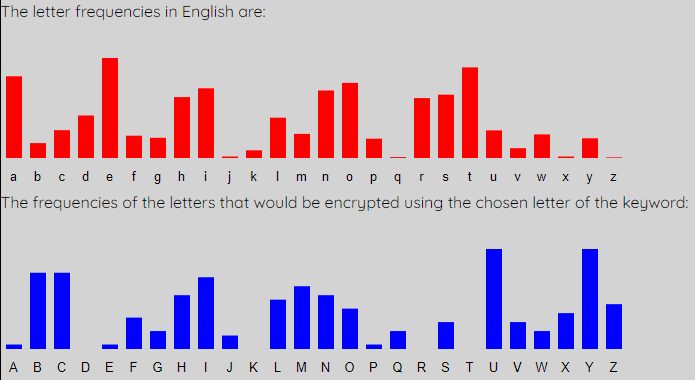
The first (red) graph shows the percentage frequency of each letter in the English language. The second (blue) graph shows the percentage frequency of each letter in the first column of the intercept. You can see that the general shape of the two graphs is very similar, but it looks like the red one has been shifted to get the blue one. We can shift the blue one along to match the expected red graph better. To do this, simply up the shift to 1.
The output when we shift the frequencies of the column by 1
Notice that the peaks and troughs of the two graphs now match pretty well. Also see that the letter of the keyword "L1" has updated to "B". This means that the first letter of the keyword is b. We also get the updated Decrypted Message, where every letter in the intercept that is encoded using this letter of the keyword is changed to what it would be if decrytped by this key letter. We get the following:
|
bVJTNAeENMCDlKBXFSsKLHGSnJWHOFtISFYFaEXEINeIMAYSrDYYIJmPWTOKeRHWVWsZFXHLtYUMSGuDURBWaIVXFAeMYFYXoIGBHWhFHHOJaEXAUNeIYLJWcKNHGAnVBHHGuINAULyFOFUQbVFBYNeTYGMMrVGXCFyFOKQAsUIFUFdRQTEWyFOKMWnJYLNZaKSHOEaPNAYTeKNXLBuUAXCXtYYKYTeRHRCFtYCLUKsVGUFQaESWYSrWLBYFdFZVUWsRLLNGhZGBMSyKBTNTrLNNMDoMYMIUaVMTLOaJHHFWsJNAUFhZMBZLhVHMBStWLBYFdUYFUFdNBRVJuKOLLGsVUZUAnJNVUWsRLMBAsZMFSSnJQXLFoKNAULiCIOYVcRYLUJlVMLVMtKBTNAlFPXXJoDYFIJeYUWSGuIUMBWrTUXMSrNYKYDiMCGASnUXBYSlCMEUNeJNAUFtYUMWSeJUKQWrVXXUVtFFBPWaCFYLWeDYGUKcRYLUJlFPXXEeZQXYHfFLACEaJBXQSsWIKNMnRNXCJeAIBWWaKCMUKhVQTMNaCCTHLiYIGIMrYCFVMtRMAYOaJUFVAtZINMAsCYPBAmKBXLWiJNXUJsWIKBAsCIOYBoPZHLZiJZHLLuEYAIFoLLYIJhZMOUDoLLTHVdVUMBXoIBBMSmSCMCGnNBHCKhVLXMGbRMXNZaKQHODdSYTVGnUGTHAfRHRMHeREYIJhZGAUNeZIYZWnUYWQZoZMAYJeJIKOVeKBTNOoLFWHGtSYTLGmRHBZSnPMIYSkWIKBAmYUOYAoWZXHVeUQAIAsYYKYKoMCEYLhRNPCDlEIMFGvVBBMUoLHMLQiWUGSKpVUDZGrYCFBSvVCHZXeEXXXApROLYXoIUKYHlPNAYFnFHXBSvVCHZXeEXXXAhRPXXGnVHHGGrVNHWSeJUKNZaESHOKhRFEXGtFVKOLuJNAYIuVMMCGnFZACKdVUMBAsVHKIDlVXBHLhVWTJAtFFACKgCIKSFoKYQNWnLUMYVwYYKYAnYYPUKwFLMBQnFLACKoWZXHUeJYGZGrTYWZGrNBBWZhVMNZXeIYWXWaKBAYJeTIFYKhZMUIVyDINLFeUVRGSrBUGNGnPQAILhFOZBZeYUWHGhRHWCFhZMWYStYMAUDlIYVYAvVNAYTeEYYCLoWBBMVyZHZUHlRWXCFtYYVIEmFHPYSlKBTMOhZWAIXyFOLBSlCHHNOiKBMBAsZXXJSrKNAULaJCLFWwDSUYKtCIOYJfFLMBWgFIWIXrFGXCZaMYMBWsRGXXSgXYKZGrDSLYDfNBXHAtJBTFDpCYTMWmPWHOFtISMIFeVXFSVeRNA
|
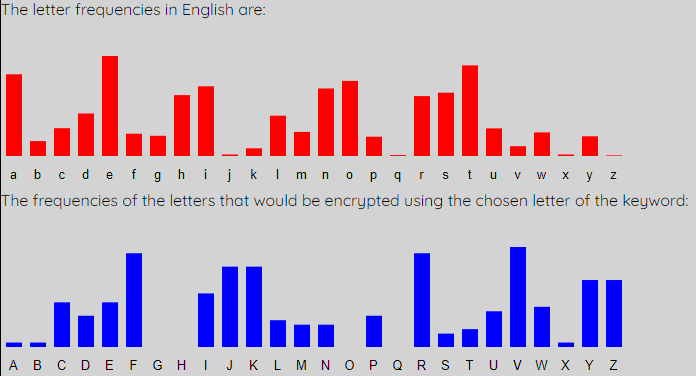
We now repeat this for the second letter of the keyword, by selecting "L2", and clicking "Check Letter". We then shift the blue graph until it most closely matches the red graph. This requires a shift of 17, and at this point the second key letter is r.
The initial frequency graphs for L2
The shifted frequency graph, after a shift of 17 to give key letter R
With this shift being used we acquire the Decrypted Message below, now with all the letters corresponding to the first and second letter of the keyword decrypted.
|
beJTNAenNMCDltBXFSstLHGSnsWHOFtrSFYFanXEINerMAYSrmYYIJmyWTOKeaHWVWsiFXHLthUMSGumURBWarVXFAevYFYXorGBHWhoHHOJanXAUNerYLJWctNHGAneBHHGurNAULyoOFUQbeFBYNecYGMMreGXCFyoOKQAsdIFUFdaQTEWyoOKMWnsYLNZatSHOEayNAYTetNXLBudAXCXthYKYTeaHRCFthCLUKseGUFQanSWYSrfLBYFdoZVUWsaLLNGhiGBMSytBTNTruNNMDovYMIUaeMTLOasHHFWssNAUFhiMBZLheHMBStfLBYFddYFUFdwBRVJutOLLGseUZUAnsNVUWsaLMBAsiMFSSnsQXLFotNAULilIOYVcaYLUJleMLVMttBTNAloPXXJomYFIJehUWSGurUMBWrcUXMSrwYKYDivCGASndXBYSllMEUNesNAUFthUMWSesUKQWreXXUVtoFBPWalFYLWemYGUKcaYLUJloPXXEeiQXYHfoLACEasBXQSsfIKNMnaNXCJejIBWWatCMUKheQTMNalCTHLihIGIMrhCFVMtaMAYOasUFVAtiINMAslYPBAmtBXLWisNXUJsfIKBAslIOYBoyZHLZisZHLLunYAIFouLYIJhiMOUDouLTHVdeUMBXorBBMSmbCMCGnwBHCKheLXMGbaMXNZatQHODdbYTVGndGTHAfaHRMHeaEYIJhiGAUNeiIYZWndYWQZoiMAYJesIKOVetBTNOouFWHGtbYTLGmaHBZSnyMIYSkfIKBAmhUOYAofZXHVedQAIAshYKYKovCEYLhaNPCDlnIMFGveBBMUouHMLQifUGSKpeUDZGrhCFBSveCHZXenXXXApaOLYXorUKYHlyNAYFnoHXBSveCHZXenXXXAhaPXXGneHHGGreNHWSesUKNZanSHOKhaFEXGtoVKOLusNAYIueMMCGnoZACKdeUMBAseHKIDleXBHLheWTJAtoFACKglIKSFotYQNWnuUMYVwhYKYAnhYPUKwoLMBQnoLACKofZXHUesYGZGrcYWZGrwBBWZheMNZXerYWXWatBAYJecIFYKhiMUIVymINLFedVRGSrkUGNGnyQAILhoOZBZehUWHGhaHWCFhiMWYSthMAUDlrYVYAveNAYTenYYCLofBBMVyiHZUHlaWXCFthYVIEmoHPYSltBTMOhiWAIXyoOLBSllHHNOitBMBAsiXXJSrtNAULasCLFWwmSUYKtlIOYJfoLMBWgoIWIXroGXCZavYMBWsaGXXSggYKZGrmSLYDfwBXHAtsBTFDplYTMWmyWHOFtrSMIFeeXFSVeaNA
|
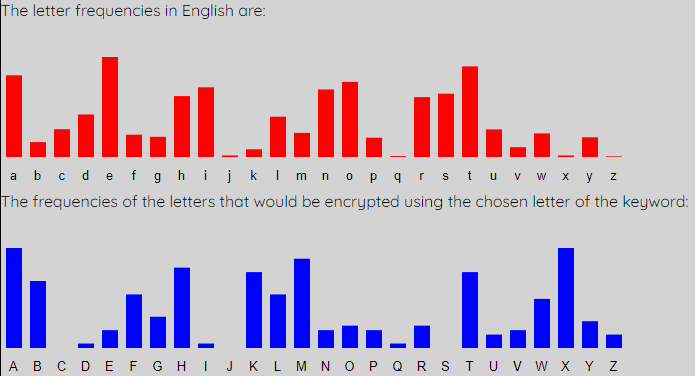
This process continues through the rest of the letters of the keyword. For L3 we get the graphs shown below, and it is a shift of 20, giving key letter u that is the best match.
The initial set up of the frequency graphs for L3
A shift of 20 produces this frequency graph
|
bepTNAentMCDlthXFSstrHGSnscHOFtryFYFandEINersAYSrmeYIJmycTOKeanWVWsilXHLthaMSGumaRBWarbXFAeveFYXormBHWhonHOJandAUNereLJWcttHGAnehHHGurtAULyouFUQbelBYNeceGMMremXCFyouKQAsdoFUFdawTEWyouKMWnseLNZatyHOEaytAYTettXLBudgXCXtheKYTeanRCFthiLUKsemUFQanyWYSrfrBYFdofVUWsarLNGhimBMSythTNTrutNMDoveMIUaesTLOasnHFWsstAUFhisBZLhenMBStfrBYFddeFUFdwhRVJutuLLGseaZUAnstVUWsarMBAsisFSSnswXLFottAULiloOYVcaeLUJlesLVMtthTNAlovXXJomeFIJehaWSGuraMBWrcaXMSrweKYDiviGASnddBYSllsEUNestAUFthaMWSesaKQWredXUVtolBPWallYLWemeGUKcaeLUJlovXXEeiwXYHforACEashXQSsfoKNMnatXCJejoBWWatiMUKhewTMNaliTHLihoGIMrhiFVMtasAYOasaFVAtioNMAslePBAmthXLWistXUJsfoKBAsloOYBoyfHLZisfHLLuneAIFourYIJhisOUDourTHVdeaMBXorhBMSmbiMCGnwhHCKherXMGbasXNZatwHODdbeTVGndmTHAfanRMHeakYIJhimAUNeioYZWndeWQZoisAYJesoKOVethTNOoulWHGtbeTLGmanBZSnysIYSkfoKBAmhaOYAoffXHVedwAIAsheKYKoviEYLhatPCDlnoMFGvehBMUounMLQifaGSKpeaDZGrhiFBSveiHZXendXXApauLYXoraKYHlytAYFnonXBSveiHZXendXXAhavXXGnenHGGretHWSesaKNZanyHOKhalEXGtobKOLustAYIuesMCGnofACKdeaMBAsenKIDledBHLhecTJAtolACKgloKSFoteQNWnuaMYVwheKYAnhePUKworMBQnorACKoffXHUeseGZGrceWZGrwhBWZhesNZXereWXWathAYJecoFYKhisUIVymoNLFedbRGSrkaGNGnywAILhouZBZehaWHGhanWCFhisWYSthsAUDlreVYAvetAYTeneYCLofhBMVyinZUHlacXCFtheVIEmonPYSlthTMOhicAIXyouLBSllnHNOithMBAsidXJSrttAULasiLFWwmyUYKtloOYJforMBWgooWIXromXCZaveMBWsamXXSggeKZGrmyLYDfwhXHAtshTFDpleTMWmycHOFtryMIFeedFSVeatA
|
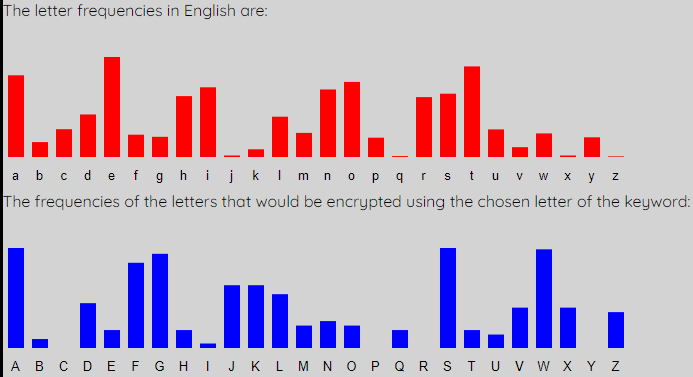
When we analyse L4, we get the following graphs which require a shift of 19, or key letter t.
The initial frequency graphs for L4
The graph for L4 needs a shift of 19 to match
|
bepaNAenttCDltheFSstroGSnscoOFtrymYFandlINershYSrmefIJmycaOKeandVWsileHLthatSGumayBWarbeFAevemYXormiHWhonoOJandhUNeresJWcttoGAnehoHGurthULyoumUQbeliYNecenMMremeCFyourQAsdomUFdawaEWyourMWnsesNZatyoOEaythYTetteLBudgeCXtherYTeanyCFthisUKsembFQanydYSrfriYFdofcUWsarsNGhimiMSythaNTrutuMDovetIUaesaLOasnoFWssthUFhisiZLhentBStfriYFddemUFdwhyVJutusLGseagUAnstcUWsartBAsismSSnsweLFotthULilovYVcaesUJlessVMtthaNAloveXJomemIJehadSGuratBWrcaeMSrwerYDivinASnddiYSllslUNesthUFthatWSesarQWredeUVtoliPWallfLWemenUKcaesUJloveXEeiweYHforhCEasheQSsforNMnateCJejoiWWatitUKhewaMNaliaHLihonIMrhimVMtashYOasamVAtiouMAslewBAmtheLWisteUJsforBAslovYBoyfoLZisfoLLunehIFourfIJhisvUDouraHVdeatBXorhiMSmbitCGnwhoCKhereMGbaseNZatwoODdbeaVGndmaHAfanyMHeakfIJhimhUNeiofZWndedQZoishYJesorOVethaNOouldHGtbeaLGmaniZSnyspYSkforBAmhavYAoffeHVedwhIAsherYKovilYLhatwCDlnotFGvehiMUountLQifanSKpeakZGrhimBSveioZXendeXApausYXorarYHlythYFnoneBSveioZXendeXAhaveXGnenoGGretoWSesarNZanyoOKhallXGtobrOLusthYIuestCGnofhCKdeatBAsenrIDlediHLhecaJAtolhCKglorSFotexNWnuatYVwherYAnhewUKwortBQnorhCKoffeHUesenZGrcedZGrwhiWZhesuZXeredXWathhYJecomYKhisbIVymouLFedbyGSrkanNGnywhILhougBZehadHGhandCFhisdYSthshUDlrecYAvethYTenefCLofhiMVyingUHlaceCFthecIEmonwYSlthaMOhichIXyousBSllnoNOithtBAsideJSrtthULasisFWwmybYKtlovYJfortBWgoodIXromeCZavetBWsameXSggerZGrmysYDfwheHAtshaFDpleaMWmycoOFtrytIFeedmSVeath
|
When we analyse L5, we find that we need a shift of 20 again, to get the fifth key letter as u. So far a keyword is brutu.
The initial graphs for L5
This time it is a shift of 20 that gets our closest match
|
bepatAenttiDlthelSstromSnscouFtrymeFandloNersheSrmefoJmycauKeandbWsilenLthatyGumayhWarbelAevemeXorminWhonouJandhaNerespWcttomAnehonGurthaLyoumaQbelieNecensMremeiFyourwAsdomaFdawakWyoursWnsestZatyouEaytheTetterBudgeiXthereTeanyiFthisaKsemblQanydeSrfrieFdofcaWsarstGhimisSythatTrutusDovetoUaesarOasnolWssthaFhisifLhenthStfrieFddemaFdwhybJutusrGseagaAnstcaWsarthAsismySnswerFotthaLiloveVcaesaJlessbMtthatAlovedJomemoJehadyGurathWrcaesSrwereDivingSnddieSllslaNesthaFthatcSesarwWredeaVtolivWallfrWemenaKcaesaJlovedEeiweeHforhiEashewSsfortMnateiJejoicWatitaKhewasNalianLihonoMrhimbMtasheOasambAtiousAslewhAmtherWisteaJsforhAsloveBoyforZisforLunehoFourfoJhisvaDouranVdeathXorhisSmbitiGnwhoiKheresGbasetZatwouDdbeabGndmanAfanysHeakfoJhimhaNeioffWndedwZoisheJesoruVethatOouldnGtbearGmanifSnyspeSkforhAmhaveAoffenVedwhoAshereKovileLhatwiDlnotlGvehisUountrQifanyKpeakfGrhimhSveiofXendedApauseXorareHlytheFnonehSveiofXendedAhavedGnenomGretocSesartZanyouKhalldGtobruLustheIuestiGnofhiKdeathAsenroDledinLhecapAtolhiKgloryFotextWnuateVwhereAnhewaKworthQnorhiKoffenUesenfGrcedfGrwhicZhesufXereddWathheJecomeKhisboVymourFedbymSrkantGnywhoLhoughZehadnGhandiFhisdeSthshaDlreceAvetheTenefiLofhisVyingaHlaceiFthecoEmonweSlthasOhichoXyoushSllnotOiththAsidepSrtthaLasislWwmybeKtloveJforthWgoodoXromeiZavethWsamedSggerfGrmyseDfwhenAtshalDpleasWmycouFtrytoFeedmyVeath
|
Finally we analyse L6 to get the graphs shown. We require a shift of 18 this time, and we retrieve our keyword brutus.
The starting graphs form L6
After a shift of 18 we get a close match to actual frequencies
|
bepatienttillthelastromanscountrymenandlovershearmeformycauseandbesilentthatyoumayhearbelievemeforminehonourandhaverespecttominehonourthatyoumaybelievecensuremeinyourwisdomandawakeyoursensesthatyoumaythebetterjudgeiftherebeanyinthisassemblyanydearfriendofcaesarstohimisaythatbrutuslovetocaesarwasnolessthanhisifthenthatfrienddemandwhybrutusroseagainstcaesarthisismyanswernotthatilovedcaesarlessbutthatilovedromemorehadyourathercaesarwerelivinganddieallslavesthanthatcaesarweredeadtoliveallfreemenascaesarlovedmeiweepforhimashewasfortunateirejoiceatitashewasvaliantihonourhimbutashewasambitiousislewhimthereistearsforhislovejoyforhisfortunehonourforhisvalouranddeathforhisambitionwhoisheresobasethatwouldbeabondmanifanyspeakforhimhaveioffendedwhoisheresorudethatwouldnotbearomanifanyspeakforhimhaveioffendedwhoisheresovilethatwillnotlovehiscountryifanyspeakforhimhaveioffendedipauseforareplythennonehaveioffendedihavedonenomoretocaesarthanyoushalldotobrutusthequestionofhisdeathisenrolledinthecapitolhisglorynotextenuatedwhereinhewasworthynorhisoffencesenforcedforwhichhesuffereddeathherecomeshisbodymournedbymarkantonywhothoughhehadnohandinhisdeathshallreceivethebenefitofhisdyingaplaceinthecommonwealthaswhichofyoushallnotwiththisidepartthatasislewmybestloverforthegoodofromeihavethesamedaggerformyselfwhenitshallpleasemycountrytoneedmydeath
|
Now we must insert spaces and punctuation to retrieve the original, which is a monologe by Brutus in "Julius Caesar" by Shakespeare.
|
Be patient till the last. Romans, countrymen, and lovers! hear me for my cause, and be silent, that you may hear: believe me for mine honour, and have respect to mine honour, that you may believe: censure me in your wisdom, and awake your senses, that you may the better judge. If there be any in this assembly, any dear friend of Caesar's, to him I say, that Brutus' love to Caesar was no less than his. If then that friend demand why Brutus rose against Caesar, this is my answer: —Not that I loved Caesar less, but that I loved Rome more. Had you rather Caesar were living and die all slaves, than that Caesar were dead, to live all free men? As Caesar loved me, I weep for him; as he was fortunate, I rejoice at it; as he was valiant, I honour him: but, as he was ambitious, I slew him. There is tears for his love; joy for his fortune; honour for his valour; and death for his ambition. Who is here so base that would be a bondman? If any, speak; for him have I offended. Who is here so rude that would not be a Roman? If any, speak; for him have I offended. Who is here so vile that will not love his country? If any, speak; for him have I offended. I pause for a reply. Then none have I offended. I have done no more to Caesar than you shall do to Brutus. The question of his death is enrolled in the Capitol; his glory not extenuated, wherein he was worthy, nor his offences enforced, for which he suffered death. Here comes his body, mourned by Mark Antony: who, though he had no hand in his death, shall receive the benefit of his dying, a place in the commonwealth; as which of you shall not? With this I depart,—that, as I slew my best lover for the good of Rome, I have the same dagger for myself, when it shall please my country to need my death.
|
In using this process we have not only recovered the plaintext, but also the keyword. This could be useful if more than one message is sent using the same keyword.
Discussion
The Kasiski Analysis is a very powerful method for Cryptanalysis, and was a major development in the field. As discussed earlier, the Vigenère Cipher was thought to be unbreakable, and as is the general trend in the history of Cryptography, this was proven not to be the case.
The Kasiski Analysis is a very powerful method for Cryptanalysis, and was a major development in the field. As discussed earlier, the Vigenère Cipher was thought to be unbreakable, and as is the general trend in the history of Cryptography, this was proven not to be the case.
As with Frequency Analysis, the intercept needs to be of a fairly long length in order for the process to work successfully, as you need n-graphs to repeat and you need to be able to use frequency analysis on parts of the message.
In terms of the development of the subject, the Kasiski Analysis method was ground breaking as it was the first new method to break a cipher for centuries. It also turned the whole war between cryptographers and cryptanalysts on its head, as the most secure cipher fell. However, this was not to remain the case, and the cryptographers would fight back with even better ciphers.