Four-Square Cipher
The Four-Square Cipher was invented by the famous French cryptographer Felix Delastelle. It is similar in nature to both the Playfair Cipher and the Two-Square Cipher (which was actually developed after the Four-Square Cipher as a simpler but less secure version).
It is a digraphic substitution cipher, and uses four grids to match the digraphs from plaintext to ciphertext and vice versa. Two of the grids are the plaintext grids which are just grids with the alphabet in order (combining "i" and "j" to get 25 letters), and the other two grids are Mixed Squares, each using a different keyword. As with the other forms of Digraph Substitution ciphers, it is significantly more secure than Monoalphabetic Substitution, but still susceptible to frequency analysis of digraphs.
Encryption
To encrypt using the Four-Square Cipher we must first split the ciphertext into digraphs (pairs of letters), and we must add an "X" to the end if the final letter is by itself. We must now create the four squares to be used in the encryption process. The top left and bottom right are the plaintext squares, and contain the letters of the alphabet in order. The top right and bottom left are the ciphertext squares, which are Mixed Squares generated using the two keywords (first keyword gives top right, second keyword gives bottom left).
To encrypt using the Four-Square Cipher we must first split the ciphertext into digraphs (pairs of letters), and we must add an "X" to the end if the final letter is by itself. We must now create the four squares to be used in the encryption process. The top left and bottom right are the plaintext squares, and contain the letters of the alphabet in order. The top right and bottom left are the ciphertext squares, which are Mixed Squares generated using the two keywords (first keyword gives top right, second keyword gives bottom left).
With the squares generated, and the plaintext split into digraphs, for each digraph, we find the first letter in the top left square, and the second letter in the bottom right square. We then form a rectangle with these two points as opposite corners. The ciphertext digraph is formed by taking the other two corners of this rectangle. The first ciphertext letter is the corner in the top right square, and the second letter is the corner in the bottom left square.
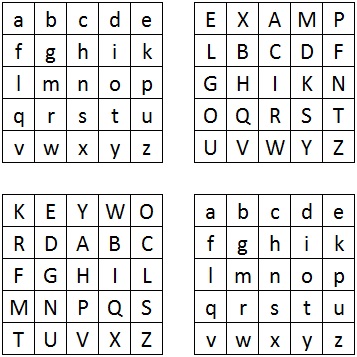
As an example we shall encrypt the plaintext "test plaintext" with the keywords example and keyword.
The first thing we need to do is split the plaintext into digraphs as below. Notice that since the final "t" would be by itself, in order to make it a digraph we must add an "x".
The plaintext "test plaintext" split into digraphs.
Now we have to generate the four squares for use in the encryption. The top left and bottom right are just the alphabet in order. As these are the plaintext squares, we write the letters in the square in lowercase. The top right square is the Mixed Square formed with the keyword example, and the bottom left square is the Mixed Square formed with the keyword keyword. Both of these are ciphertext squares, so we use uppercase letters.
The Four-Square layout using the keywords "example" and "keyword".
For each digraph of the plaintext, you locate the first letter in the top left square, and the second letter in the bottom right square. You then form the rectangle that has these two points as opposite corners. The other two corners form the ciphertext digraph, and you take the corner in the top right square as the first letter, and the corner in the bottom left square as the second letter.
Now we just need to collect all the ciphertext digraphs.
The final ciphertext digraphs.
Finally we write out the ciphertext "TWSPGLMRKPAZRX", or if you want to keep the structure of the original "TWSP GLMRKPAZRX".
Decryption
Decryption is much the same as encryption, but as we start with ciphertext, we locate in the ciphertext squares, and read from the plaintext squares.
Decryption is much the same as encryption, but as we start with ciphertext, we locate in the ciphertext squares, and read from the plaintext squares.
Firstly we must split the ciphertext into digraphs, and create the four squares needed, as with encryption. Now for each ciphertext digraph, you find the first letter in the top right square, and the second letter in the bottom left square. You form the rectangle with these two points as corners. The corner that is in the top left square is the first letter of the plaintext, and the corner that is in the bottom right square is the second letter of the plaintext.
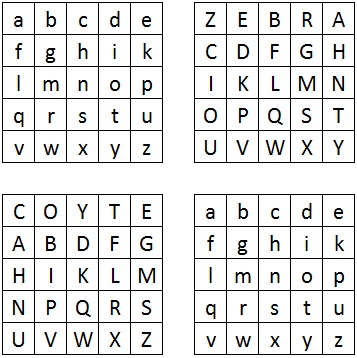
As an example, we shall decrypt the ciphertext "NCZUB MKX" with the keywords zebra and coyote.
First we must split the ciphertext into the digraphs.
The ciphertext split into digraphs.
And we need to generate the four squares.
The Four Square layout
Now, for each digraph, we locate the first ciphertext letter in the top right square, and the second letter in the bottom left square. We now form the rectangle with these two points as corners. The corner of this rectangle which is in the top left square is the first plaintext letter, and the corner which is in the bottom right square is the second plaintext letter.
Putting together all the digraphs we get:
And finally we read off the plaintext of "leave now".
Discussion
Cryptanalysis of the Four-Square Cipher is similar to other Digraph Substitution Ciphers. You can perform frequency analysis on the digraphs (though there are 676 possibilities rather than the 26 possibles choices for Monoalphabetic Substitution Ciphers). The Four-Square cipher is stronger than the Playfair Cipher in that it can encrypt double letters, and can obtain them in the ciphertext as well. It can also encrypt a plaintext letter to itself (a transparency), which the Playfair cannot do.
Cryptanalysis of the Four-Square Cipher is similar to other Digraph Substitution Ciphers. You can perform frequency analysis on the digraphs (though there are 676 possibilities rather than the 26 possibles choices for Monoalphabetic Substitution Ciphers). The Four-Square cipher is stronger than the Playfair Cipher in that it can encrypt double letters, and can obtain them in the ciphertext as well. It can also encrypt a plaintext letter to itself (a transparency), which the Playfair cannot do.
However, on weakness of the Four-Square which can be utilised by a cryptanalyst is that in certain words, the same ciphertext letter will be produced no matter the keyword. For example, in the word "mi li ta ry", no matter what keywords we pick the first and third ciphertext letters will be the same. This is because "l" and "m" are on the same row in the plaintext square, and they both have "i" forming the other corner. So the corner in the top right square will be the same (although the other corner will be different).
This boils down to the fact that if two ciphertext letters are the same (in the first position of a digraph), then the first letters must be in the same row as each other, and the second letters must be in the same column as each other in the plaintext squares. And since we know the plaintext squares, we can eliminate possibilities.
One way to overcome this weakness is to use Mixed Squares for each of the plaintext squares as well. This jumbles up the order of the letters in the top left and bottom right squares, so that it is not possible to guess that two letters are on the same row.