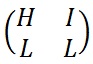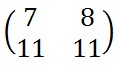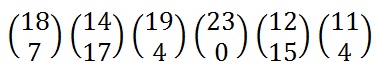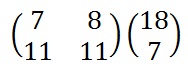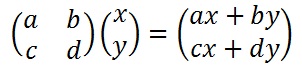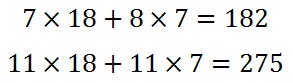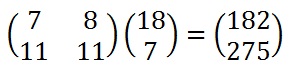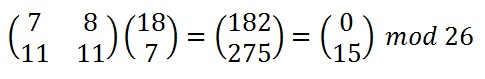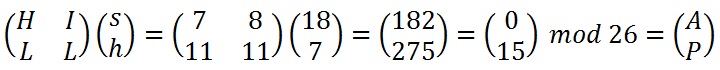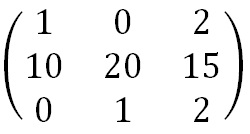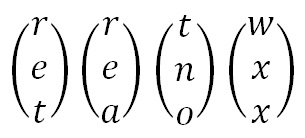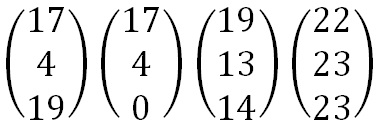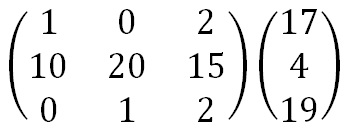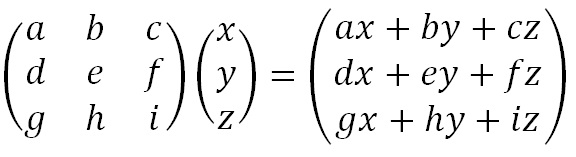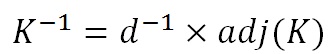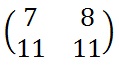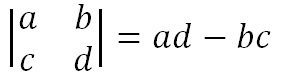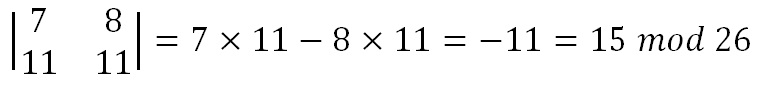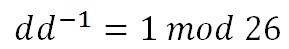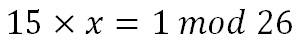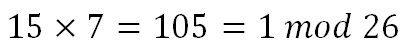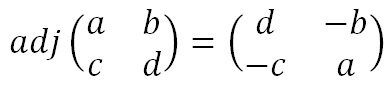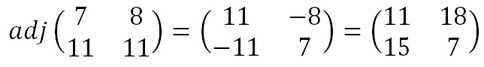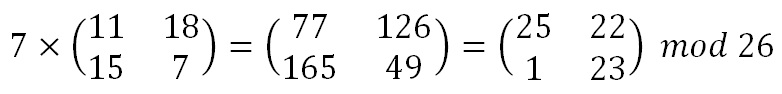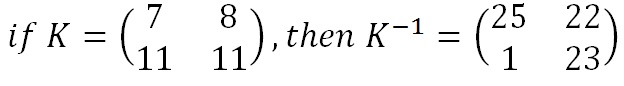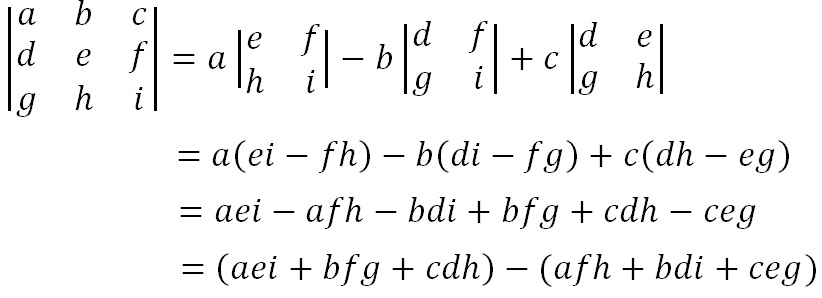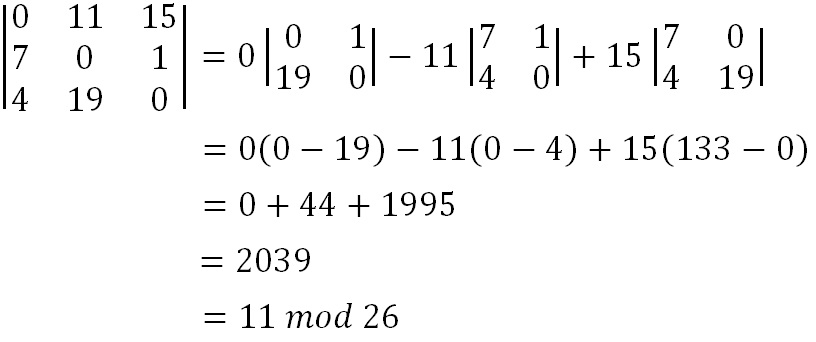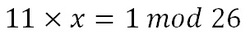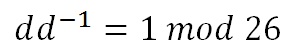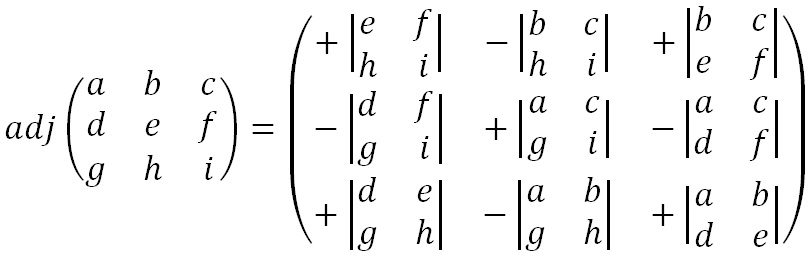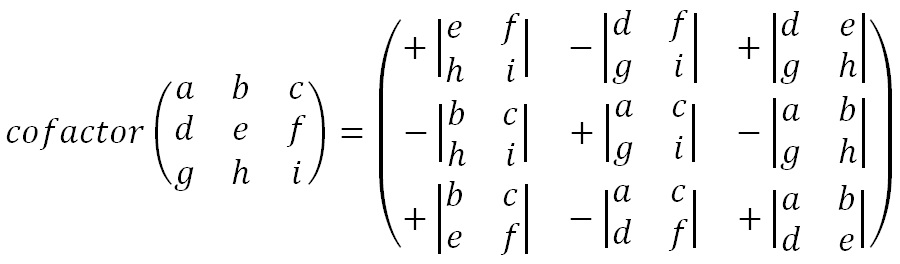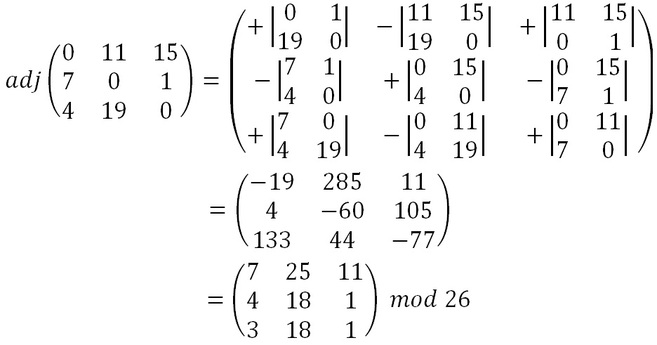Hill Cipher
The Hill Cipher was invented by Lester S. Hill in 1929, and like the other Digraphic Ciphers it acts on groups of letters. Unlike the others though it is extendable to work on different sized blocks of letters. So, technically it is a polygraphic substitution cipher, as it can work on digraphs, trigraphs (3 letter blocks) or theoretically any sized blocks.
The Hill Cipher uses an area of mathematics called Linear Algebra, and in particular requires the user to have an elementary understanding of matrices. It also make use of Modulo Arithmetic (like the Affine Cipher). Because of this, the cipher has a significantly more mathematical nature than some of the others. However, it is this nature that allows it to act (relatively) easily on larger blocks of letters.
In the examples given, we shall walk through all the steps to use this cipher to act on digraphs and trigraphs. It can be extended further, but this then requires a much deeper knowledge of the background mathematics. Some important concepts are used throughout: Matrix Multiplication; Modular Inverses; Determinants of Matrices; Matrix Adjugates (for finding inverses).
Encryption
To encrypt a message using the Hill Cipher we must first turn our keyword into a key matrix (a 2 x 2 matrix for working with digraphs, a 3 x 3 matrix for working with trigraphs, etc). We also turn the plaintext into digraphs (or trigraphs) and each of these into a column vector. We then perform matrix multiplication modulo the length of the alphabet (i.e. 26) on each vector. These vectors are then converted back into letters to produce the ciphertext.
To encrypt a message using the Hill Cipher we must first turn our keyword into a key matrix (a 2 x 2 matrix for working with digraphs, a 3 x 3 matrix for working with trigraphs, etc). We also turn the plaintext into digraphs (or trigraphs) and each of these into a column vector. We then perform matrix multiplication modulo the length of the alphabet (i.e. 26) on each vector. These vectors are then converted back into letters to produce the ciphertext.
|
2 x 2 Example
We shall encrypt the plaintext message "short example" using the keyword hill and a 2 x 2 matrix. The first step is to turn the keyword into a matrix. If the keyword was longer than the 4 letters needed, we would only take the first 4 letters, and if it was shorter, we would fill it up with the alphabet in order (much like a Mixed Alphabet). |
The keyword written as a matrix.
|
|
With the keyword in a matrix, we need to convert this into a key matrix. We do this by converting each letter into a number by its position in the alphabet (starting at 0). So, A = 0, B = 1, C= 2, D = 3, etc.
|
The key matrix (each letter of the keyword is converted to a number).
|
We now split the plaintext into digraphs, and write these as column vectors. That is, in the first column vector we write the first plaintext letter at the top, and the second letter at the bottom. Then we move to the next column vector, where the third plaintext letter goes at the top, and the fourth at the bottom. This continues for the whole plaintext.
The plaintext "short example" split into column vectors.
Now we must convert the plaintext column vectors in the same way that we converted the keyword into the key matrix. Each letter is replaced by its appropriate number.
The plaintext converted into numeric column vectors.
Now we must perform some matrix multiplication. We multiply the key matrix by each column vector in turn. We shall go through the first of these in detail, then the rest shall be presented in less detail. We write the key matrix first, followed by the column vector.
To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the bottom row of the key matrix with the column vector to get the bottom element of the resulting column vector. The way we "combine" the four numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, and multiply the second element of the key matrix row by the bottom element of the column vector. We then add together these two answers.
The algebraic rules of matrix multiplication.
|
That is, we follow the rules given by the algebraic method shown to the left.
|
|
In our case we perform the two calculations on the right. We then right these two answers out in a column vector as shown below.
|
The calculations performed when doing a matrix multiplication.
|
The shorthand for the matrix multiplication.
Next we have to take each of these numbers, in our resultant column vector, modulo 26 (remember that means divide by 26 and take the remainder).
Reducing the resultant column vector modulo 26.
Finally we have to convert these numbers back to letters, so 0 becomes "A" and 15 becomes "P", and our first two letters of the ciphertext are "AP".
The whole calculation: converting to numbers; the matrix multiplication; reducing modulo 26; converting back to letters.
This gives us a final ciphertext of "APADJ TFTWLFJ".
|
3 x 3 Example
We shall encrypt the plaintext message "retreat now" using the keyphrase back up and a 3 x 3 matrix. The first step is to turn the key phrase into a matrix. Notice that the key phrase is a few letters short, so we fill in the final elements with the start of the alphabet. |
The keyword written as a matrix.
|
|
Now we turn the keyword matrix into the key matrix by replacing letters with their numeric values.
|
The Key Matrix obtained by taking the numeric values of the letters of the key phrase.
|
Now we split the plaintext into trigraphs (we are using a 3 x 3 matrix so we need groups of 3 letters), and convert these into column vectors. However, since the plaintext does not go perfectly into the column vectors, we need to use some nulls to make the plaintext the right length. We then convert these into numeric column vectors.
The plaintext split into trigraphs and written in column vectors. Note the nulls added to make it the right length
|
The plaintext converted into numeric column vectors.
|
|
Now we perform matrix multiplication, multiplying the key matrix by each column vector in turn. To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the middle row of the key matrix with the column vector to get the middle element of the resulting column vector. and similarly for the bottom row. The way we "combine" the six numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, multiply the second element of the key matrix row by the middle element of the column vector, and multiply the third element of the key matrix row by the bottom element of the column vector. We then add together these three answers.
|
The first matrix mltiplication.
|
Algebraic representation of matrix multiplication for a 3 x 3 matrix.
We then follow the same process as for the 2 x 2 Matrix Example. We perform all the matrix multiplcations, and take the column vectors modulo 26. Then we convert them back into letters to produce the ciphertext.
This gives us a final ciphertext of "DPQRQ EVKPQ LR".
Decryption
To decrypt a ciphertext encoded using the Hill Cipher, we must find the inverse matrix. Once we have the inverse matrix, the process is the same as encrypting. That is we multiply the inverse key matrix by the column vectors that the ciphertext is split into, take the results modulo the length of the alphabet, and finally convert the numbers back to letters.
To decrypt a ciphertext encoded using the Hill Cipher, we must find the inverse matrix. Once we have the inverse matrix, the process is the same as encrypting. That is we multiply the inverse key matrix by the column vectors that the ciphertext is split into, take the results modulo the length of the alphabet, and finally convert the numbers back to letters.
Since the majority of the process is the same as encryption, we are going ot focus on finding the inverse key matrix (not an easy task), and will then skim quickly through the other steps (for more information see Encryption above).
In general, to find the inverse of the key matrix, we perform the calculation below, where K is the key matrix, d is the determinant of the key matrix and adj(K) is the adjugate matrix of K.
General method to calculate the inverse key matrix.
|
2 x 2 Example
We shall decrypt the example above, so we are using the keyword hill and our ciphertext is "APADJ TFTWLFJ". We start by writing out the keyword as a matrix and converting this into a key matrix as for encryption. Now we must convert this to the inverse key matrix, for which there are several steps. |
The keyword written as a matrix.
The key matrix (each letter of the keyword is converted to a number).
|
Step 1 - Find the Multiplicative Inverse of the Determinant
The determinant is a number that relates directly to the entries of the matrix. It is found by multiplying the top left number by the bottom right number and subtracting from this the product of the top right number and the bottom left number. This is shown algebraically below. Note that the notation for determinant has straight lines instead of brackets around our matrix.
The determinant is a number that relates directly to the entries of the matrix. It is found by multiplying the top left number by the bottom right number and subtracting from this the product of the top right number and the bottom left number. This is shown algebraically below. Note that the notation for determinant has straight lines instead of brackets around our matrix.
Algebraic method to calculate the determinant of a 2 x 2 matrix.
Once we have found this value, we need to take the number modulo 26. Below is the way to calculate the determinant for our example.
Calculating the determinant of our 2 x 2 key matrix.
|
We now have to find the multiplicative inverse of the determinant working modulo 26. That is, the number between 1 and 25 that gives an answer of 1 when we multiply it by the determinant. So, in this case, we are looking for the number that we need to multiply 15 by to get an answer of 1 modulo 26. There are algorithms to calculate this, but it is often easiest to use trial and error to find the inverse.
|
If d is the determinant, then we are looking for the inverse of d.
The multiplicative inverse is the number we multiply 15 by to get 1 modulo 26.
|
This calculation gives us an answer of 1 modulo 26.
So the multiplicative inverse of the determinant modulo 26 is 7. We shall need this number later.
Step 2 - Find the Adjugate Matrix
The adjugate matrix is a matrix of the same size as the original. For a 2 x 2 matrix, this is fairly straightforward as it is just moving the elements to different positions and changing a couple of signs. That is, we swap the top left and bottom right numbers in the key matrix, and change the sign of the the top right and bottom left numbers. Algebraically this is given below.
The adjugate matrix is a matrix of the same size as the original. For a 2 x 2 matrix, this is fairly straightforward as it is just moving the elements to different positions and changing a couple of signs. That is, we swap the top left and bottom right numbers in the key matrix, and change the sign of the the top right and bottom left numbers. Algebraically this is given below.
The adjugate matrix of a 2 x 2 matrix.
Again, once we have these values we will need to take each of them modulo 26 (in particular, we need to add 26 to the negative values to get a number between 0 and 25. For our example we get the matrix below.
The adjugate matrix of the key matrix.
Step 3 - Multiply the Multiplicative Inverse of the Determinant by the Adjugate Matrix
To get the inverse key matrix, we now multiply the inverse determinant (that was 7 in our case) from step 1 by each of the elements of the adjugate matrix from step 2. Then we take each of these answers modulo 26.
To get the inverse key matrix, we now multiply the inverse determinant (that was 7 in our case) from step 1 by each of the elements of the adjugate matrix from step 2. Then we take each of these answers modulo 26.
Multiplying the multiplicative inverse of the determinant by the adjugate to get the inverse key matrix.
NB - note that the 165 should read 105.
That is:
Now we have the inverse key matrix, we have to convert the ciphertext into column vectors and multiply the inverse matrix by each column vector in turn, take the results modulo 26 and convert these back into letters to get the plaintext.
We get back our plaintext of "short example".
|
3 x 3 Example
We shall decrypt the ciphertext message "SYICHOLER" using the keyword alphabet. The first step is to turn the key phrase into a matrix. Notice that the keyword is a letter short, so we fill in the final element with the start of the alphabet. Now we need to convert this into the inverse key matrix, following the same step as for a 2 x 2 matrix. However, the way we calculate each step is slightly different. |
The keyword written as a matrix.
The key matrix.
|
Step 1 - Find the Multiplicative Inverse of the Determinant
The determinant is a number that relates directly to the entries of the matrix. For a 3 x 3 matrix it is found by multiplying the top left entry by the determinant of the 2 x 2 matrix formed by the entries that are not in the same row or column as that entry (that is the 2 x 2 matrix not including the top row or left column). Similar steps are done with the other two elements in the top row, and the middle value is subtracted from the sum of the other two. This is shown more clearly in the algebraic version below.
The determinant is a number that relates directly to the entries of the matrix. For a 3 x 3 matrix it is found by multiplying the top left entry by the determinant of the 2 x 2 matrix formed by the entries that are not in the same row or column as that entry (that is the 2 x 2 matrix not including the top row or left column). Similar steps are done with the other two elements in the top row, and the middle value is subtracted from the sum of the other two. This is shown more clearly in the algebraic version below.
The algebraic representation of finding the determinant of a 3 x 3 matrix.
Once we have calculated this value, we take it modulo 26.
Finding the determinant of the 3 x 3 matrix with keyword alphabet.
|
We now have to find the multiplicative inverse of the determinant working modulo 26. That is, the number between 1 and 25 that gives an answer of 1 when we multiply it by the determinant. So, in this case, we are looking for the number that we need to multiply 11 by to get an answer of 1 modulo 26. There are algorithms to calculate this, but it is often easiest to use trial and error to find the inverse.
|
The multiplicative inverse is the number we multiply 11 by to get 1 modulo 26.
If d is the determinant, then we are looking for the inverse of d.
|
Finding the multiplicative inverse of 11 modulo 26.
So the multiplicative inverse of the determinant modulo 26 is 19. We shall need this number later.
Step 2 - Find the Adjugate Matrix
The adjugate matrix is a matrix of the same size as the original. For a 3 x 3 matrix this process is somewhat more complex than it was for a 2 x 2 matrix. It requires us to calculate 9 lots of 2 x 2 determinants, and assign them with the correct signs, and put them in the correct places. The algebraic representation is given below.
The adjugate matrix is a matrix of the same size as the original. For a 3 x 3 matrix this process is somewhat more complex than it was for a 2 x 2 matrix. It requires us to calculate 9 lots of 2 x 2 determinants, and assign them with the correct signs, and put them in the correct places. The algebraic representation is given below.
Calculating the adjugate matrix of a 3 x 3 matrix.
Although this seems a bit of a random selection of letters to place in each of the discriminants, it is defined as the transpose of the cofactor matrix, which is much easier to remember how to work out. To find the cofactor matrix, we take the 2 x 2 determinant in each position such that the four values in that position are the four values not in the same row or column as the position in the original matrix. The adjugate is then formed by reflecting the cofactor matrix along the line from top left ot bottom right.
The cofactor matrix can be used to find the adjugate matrix. Simply reflect it along the line from top left ot bottom right of the matrix.
We also need to remember to take each of our values in the adjugate matrix modulo 26. So for our example we get the working below.
Calculating the adjugate matrix of the key matrix.
Step 3 - Multiply the Multiplicative Inverse of the Determinant by the Adjugate Matrix
To get the inverse key matrix, we now multiply the inverse determinant (that was 19 in our case) from step 1 by each of the elements of the adjugate matrix from step 2. Then we take each of these answers modulo 26.
To get the inverse key matrix, we now multiply the inverse determinant (that was 19 in our case) from step 1 by each of the elements of the adjugate matrix from step 2. Then we take each of these answers modulo 26.
Multiplying the inverse of the determinant by the adjugate matrix gets the inverse key matrix.
That is:
The final relationship between the key matrix and the inverse key matrix.
Finally, now we have the inverse key matrix, we multiply this by each
And we retreive our plaintext of "we are safe".
Discussion
The most important item that must be discussed regarding the use of the Hill Cipher is that not every possible matrix is a possible key matrix. This is because, in order to decrypt, we need to have an inverse key matrix, and not every matrix is invertible. Fortunately, we do not have to work out the entire inverse to find it is not possible, but simply consider the determinant. If the determinant is 0 or shares a factor, other than 1, with the length of the alphabet being used, then the matrix will not have an inverse. If this is the case, a different key must be chosen, since otherwise the ciphertext will not be able to be decrypted. In order to be a usable key, the matrix must have a non-zero determinant which is coprime to the length of the alphabet.
The most important item that must be discussed regarding the use of the Hill Cipher is that not every possible matrix is a possible key matrix. This is because, in order to decrypt, we need to have an inverse key matrix, and not every matrix is invertible. Fortunately, we do not have to work out the entire inverse to find it is not possible, but simply consider the determinant. If the determinant is 0 or shares a factor, other than 1, with the length of the alphabet being used, then the matrix will not have an inverse. If this is the case, a different key must be chosen, since otherwise the ciphertext will not be able to be decrypted. In order to be a usable key, the matrix must have a non-zero determinant which is coprime to the length of the alphabet.
The Hill Cipher requires a much larger use of mathematics than most other classical ciphers. The processes involved are relatively complex, but there are simply algorithms that need to be implemented. The process of matrix multiplication involves only multiplication and addition. Finding an inverse is somewhat more complicated (especially for a 3 x 3 matrix), and the activity below allows you to practice working these out.
The security of a 2 x 2 Hill Cipher is similar (actually slightly weaker) than the Bifid or Playfair Ciphers, and it is somewhat more laborious to implement by paper and pencil mmethods. However, as the key matrix size increases, so does the security, and also the complexity of operating the cipher. It is possible to increase the key size further than the 3 x 3 we have discussed here, but the mathematics involved gets rapidly more complex. Hill invented a machine that would mechanically implement a 6 x 6 version of the cipher, which was very secure. Unfortunately, the machine was unable to change the key setting, leaving it with limited use in the real world.
Cryptanalysis of an intercept encrypted using the Hill Cipher is certainly possible, especially for small key sizes. For the 2 x 2 version, looking for repeated digraphs would be the first step, and matching the most common ciphertext digraph to the most common digraph in English ("th") and then the second to the second most common in English ("he") would allow the interceptor to put together a possible key matrix acting on those four letters. This cou