Other Examples
Running Key
The Running Key Cipher uses another way to generate the keystream to use with the Tabula Recta. Rather than using a keyword, the running key cipher uses a key text or key book, which is agreed upon by both parties before any encryption takes place. The keystream is taken from this book, choosing a page and line number to start at. This is then referenced in a known way within the ciphertext itself, to let the receiver know where to start their keystream from.
The Running Key Cipher uses another way to generate the keystream to use with the Tabula Recta. Rather than using a keyword, the running key cipher uses a key text or key book, which is agreed upon by both parties before any encryption takes place. The keystream is taken from this book, choosing a page and line number to start at. This is then referenced in a known way within the ciphertext itself, to let the receiver know where to start their keystream from.
As an example, we shall encode the message "where shall we meet and at what time". The book we have agreed upon is The Code Book by Simon Singh, and we decide to start at page 45, line 1, for centuries, the simple monoalphabetic substitution cipher had been sufficient to ensure secrecy.
The keystream is taken from The Code Book by Simon Singh. The ciphertext is then found using a Tabula Recta.
The final step is to use some way to refer to the page number. We could use the letters A-J to be the numbers 0-9, so 45 would be "EF" and 1 would be "B". Putting this together (along with some nulls to make it harder to crack), we get XEFMB (null,4,5,null,1). This is called an indicator block.
We could then put this at the beginning or end of the ciphertext. Or, we could break the ciphertext into blocks of 5, and put this as the penultimate block. Any method is fine, so long as both parties are aware of what is being used. With this method, the final ciphertext would be: "BVVTI FAUCT AWFLI LIZSL XIVNH XEFMB TTBLX".
You can use the activity above to encrypt using the Running Key Cipher, by typing the key text from the book you have chosen in the key box (making sure it is at least as long as the plaintext). You will have to add your own indicator block.
The Running Key Cipher is quite secure, and does not suffer the same weaknesses as either the Vigenère Cipher (no repeating keystream) or the Autokey Cipher (the plaintext can't be used to get information). However, it is still possible to crack the cipher. Similarly to the Autokey, we can assume that certain words will appear within the keystream, and use this to find plausible bits of plaintext. By assimilating lots of information attained in this way, the cryptanalyst can piece together bits of plaintext, and use this to work out bits of the keystream (and vice versa).
This weakness is due to the personality of a language, and skilled cryptanalysts can utilise this. To try to get round this problem, the KGB suggested their agents used almanacs and other documants that contained a lot of data or lists, which did not have sentence structure. These are still breakable though, with time and effort.
The Beaufort Cipher
The Beaufort Cipher is a close relation to the Vigenère Cipher, and was invented by Sir Richard Beaufort. As with the Vigenère Cipher, a keyword is used, and it is repeated to create the keystream. The difference is in how the Tabula Recta is used to get to the ciphertext letter.
The Beaufort Cipher is a close relation to the Vigenère Cipher, and was invented by Sir Richard Beaufort. As with the Vigenère Cipher, a keyword is used, and it is repeated to create the keystream. The difference is in how the Tabula Recta is used to get to the ciphertext letter.
Rather than find the keystream across the top, and the plaintext down the side, and find the intersection (as in the Vigenère Cipher), we locate the plaintext letter across the top (or down the side), and go down this column until we find the keystream letter. We then take the plaintext letter to be the letter at the far left of this row.
|
For example, if we want to encrypt the plaintext letter "d" with the keystream letter m, then we:
|
The Beaufort Cipher uses the Tabula Recta in a slightly different way.
|
Due to the symmetric nature of the Tabula Recta, decrypting the Beaufort Cipher uses an identical method to the encryption process.
Notice that if we used the Vigenère Cipher with the same constraints (plaintext letter "d", keystream letter m), then we get the different ciphertext letter of "P". Also, if we were to take the keystream letter at the top, and go down to find the plaintext letter, we would again get something different, this time "R" (but using this way does not have the same decryption method).
Again, due to the symmetric properties of the Tabula Recta, there is a very close relationship between the Vigenère Cipher and the Beaufort Cipher. In fact, if you perform an Atbash Cipher on the plaintext and then encrypt with the Vigenère Cipher, you get the same result as if you just used the Beaufort Cipher (with the same keyword). Similarly for decrypting, to decrypt a message encoded with the Beaufort, we can use the Atbash on the ciphertext, and then decrypt using the Vigenère Cipher.
The One-Time Pad
The One-Time Pad (OTP) is the cryptographers dream. It was first described in 1882 by Frank Miller, but was not patented unti 1917 by Gilbert Vernam. It is so special as a cipher because it offers perfect secrecy. That is, the ciphertext offers no extra information to the cryptanalyst other than the maximum possible length of the plaintext. This was proved mathematically by Claude Shannon in 1949. We shall discuss why after we have seen how it works.
The One-Time Pad (OTP) is the cryptographers dream. It was first described in 1882 by Frank Miller, but was not patented unti 1917 by Gilbert Vernam. It is so special as a cipher because it offers perfect secrecy. That is, the ciphertext offers no extra information to the cryptanalyst other than the maximum possible length of the plaintext. This was proved mathematically by Claude Shannon in 1949. We shall discuss why after we have seen how it works.
The basic premise of the OTP is that the key is truly random. One simple way to do this is to have a Scrabble bag with one of each letter in the bag, and to take a letter, write it down, and return the letter to the bag. The other important aspect of the key is that it must be as long as the plaintext, and not repeating (like the Vigenère Cipher).
With a truly random keystream, you can then use the Tabula Recta to encrypt the plaintext, just as with the other Polyalphabetic ciphers we have seen.
|
As an example, we shall encrypt the simple message "hello" using the random keystream jqxyt.
We get the ciphertext "QUIJH".
|
The OTP works similarly to the Vigenère Cipher.
|
To decrypt the message, with the key, we follow the same method as for all our other polyalphabetic ciphers.
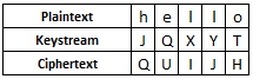
The strength is shown when we try to break it. If we had infinite computing power, we could find the the ciphertext "QUIJH" produces plaintext "hello" with the keystream jqxyt. However, we would also find that the ciphertext "QUIJH" produces the plaintext "later" with keystream fupfq. Or that the ciphertext "QUIJH" gives the plaintext "table" with the keystream xuhyd.
In fact, we can create ANY five letter word from the ciphertext "QUIJH" by choosing particular keystreams. The perfect secrecy does not rely on an interceptor not being able to get the correct message, it relies on them being able to get infinitely many possible correct messages, and for them to not be able to know which is the right one.
You can use the activity above to encrypt and decrypt messages by creating a "random" keystream, which will be as long as the plaintext. Use it to check the different keys and plaintexts acquired above.
The One-Time Pad is only perfectly secure providing certain criteria are met: the keystream must be truly random; the keystream must never be reused; the keystream must be at least as long as the plaintext; the keystream must be kept secret. Unfortunately, some of these criteria cause logistal problems for the use of the OTP.
Creating a truly random keystream is not a trivial task. When a computer creates a "random" list of numbers, it is not truly random, but pseudo-random. This means that, although it appears random to the human eye, another computer can recreate the process to get from one number to the next. In reality, the easiest way to actually generate truly random keystreams is to use the Scrabble bag described above!
The keystream must never be reused (hence the name one-time) is easy enough in theory, but in practical terms, it means that each time you want to send a message you need a new truly random keystream (and this is hard work as we saw above).
The keystream must be as long as the plaintext means that our key has to be long. If we have a plaintext that is a page long, then we need a keystream of random letters that is also a page long. This is near impossible to remember, and so must be written down, which leads to our final problem.
Keeping the keystream secret is no easy task. Due to the random nature of the keystream and its length, the keystream needs to be recorded somewhere. If you generate a random key yourself, you must send this to the receiver. This produces a huge security risk, as anyone who gets hold of the keystream can decipher the ciphertext easily. In order to share the key, you need a perfectly secure form of communication, and if this was possible, then you could send the plaintext without encrypting it. In reality, some form of steganography is usually used in this step.
For these reasons, although the OTP is theoretically unbreakable, in practical terms there are still problems with the use of the cipher.
The OTP has been used on several occasions as a practical field cipher. If using it, an agent and his handler would have the only two copies of a pad (hence one-time pad) filled with pages of random keystream. They would agree in person on how to use the pad (next sheet, reliant on the date, etc.), and when they had used a sheet to encrypt/decrypt a message, they would remove the sheet and burn it.