Myszkowski Transposition Cipher
The Myszkowski Transposition Cipher is a variant of Columnar Transposition in the way it deals with recurring letters in the keyword. It was proposed by Émile Victor Théodore Myszkowski in 1902.
The same methodology as for Columnar Transposition is used, where the plaintext is written out in rows under the keyword. The only difference is that when there are repeated letters in the keyword, rather than number them from left to right, you give all the same letters the same number. You then read across columns which have the same number in the keyword.
Encryption
We have to choose our keyword for the encryption process first. We then write out the plaintext in a grid, where the number of columns in the grid is the number of letters in the keyword. We then number each letter in the keyword with its alphabetical position, giving repeated letters the same numbers. We then start at number 1 (the first letter alphabetically in the keyword), and if it is the only appearance of 1, we read down the column just like in Columnar Transposition. If, however, the number 1 appears more than once, we read from left to right all the first letters of the columns headed by 1. Then we move to the next row, and read across, left to right, the letters in the rows headed by 1. Once complete, we move on to the number 2, and so on.
We have to choose our keyword for the encryption process first. We then write out the plaintext in a grid, where the number of columns in the grid is the number of letters in the keyword. We then number each letter in the keyword with its alphabetical position, giving repeated letters the same numbers. We then start at number 1 (the first letter alphabetically in the keyword), and if it is the only appearance of 1, we read down the column just like in Columnar Transposition. If, however, the number 1 appears more than once, we read from left to right all the first letters of the columns headed by 1. Then we move to the next row, and read across, left to right, the letters in the rows headed by 1. Once complete, we move on to the number 2, and so on.
As an example we shall use the same plaintext and keyword as we did for Columnar Transposition. That is, the plaintext is "The tomato is a plant in the nightshade family", and the keyword is tomato.
The plaintext is written in a grid beneath the keyword. The numbers represent the alphabetical order of the keyword letter, and tells us the order in which the columns will be read.
|
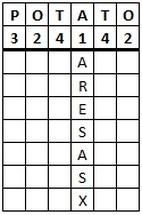
At the top of the grid, the keyword is written, to show how many columns there needs to be in the grid. Beneath this are the numbers giving the alphabetical order of the letters of the keyword. Notice that the two "O"s are both numbered 3, and the "T"s 4. This is the difference compared with Columnar Transposition.
|
We start with the column headed by 1, and since there is only one 1, we read off the column "TINESAX". The number 2 column similarly gives us "EOAHTFX". Now there are two number 3 columns, so we read the first letter from each column, left to right ("HM"), followed by each subsequent row in those two columns to get "HMTALITIHAEIYX". Finally, we do the same for the number 4 columns, to get the final ciphertext "TINES AXEOA HTFXH MTALI TIHAE IYXTO ASPTN NGHDM LX".
Decryption
Again, the decryption process is very similar to Columnar Transposition. We shall go through how to do it if nulls have been used to fill spaces. By comparing this method with that given in Columnar Transpsotion when nulls are not used, you should be able to work out what to do.
Again, the decryption process is very similar to Columnar Transposition. We shall go through how to do it if nulls have been used to fill spaces. By comparing this method with that given in Columnar Transpsotion when nulls are not used, you should be able to work out what to do.
We start by writing out the keyword, and the alphabetical order of the letters, remembering to give repeated letters the same number. We then divide the length of the ciphertext by the length of the keyword to work out how many rows we need to add to our grid. We then have to systematically put the ciphertext back in to the grid. Start at number 1, and continue to the highest number. If the number only appears once, we fill down the column. If the number appears twice, we move from left to right across the columns with that number heading them.
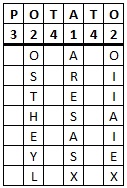
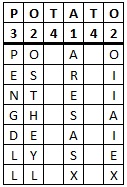
As an example, we shall decrypt the ciphertext "ARESA SXOOS ITIHA EIYEL XPENG DLLTT AEHNT HFMAW XX" given the keyword potato. We start by writing out the keyword and the order of letters. There are 42 letters in the ciphertext, and 6 letters in the keyword, so we need to add 42 ÷ 6 = 7 rows.
We put the keyword at the top of our grid, with the numerical order of the letters. We know there are 7 rows needed in our grid.
|
We start at column number 1. Since there is only one 1, we just fill down the column with the first 7 letters of the ciphertext.
|
|
The next two letters go into the first row of the two columns headed by the number 2.
|
Now we move to the columns headed by 2. There are two of them so we place the next two ciphertext letters in these columns, going from left to right.
We continue in this way down these two columns.
|
Continuing down the number 2 columns we get to this point.
|
The number 3 column is a single column, so we just add the letters down the column.
|
Finally, we add the last two columns, which both have the heading 4, so we once again put the letters in left to right.
|
Now we read off the plaintext by reading across one row at a time to get "potatoes are in the nightshade family as well".
Discussion
The Myszkowski Transposition Cipher has all the same advantages and disadvantages as Columnar Transposition. It is slightly less susceptible to be broken using anagraming, since the pattern of transposition is not as repetitive.
The Myszkowski Transposition Cipher has all the same advantages and disadvantages as Columnar Transposition. It is slightly less susceptible to be broken using anagraming, since the pattern of transposition is not as repetitive.
It is also possible to perform the Myszkowski Transposition Cipher more than once, and using multiple iterations does make it more secure, especially if using keywords of different lengths for each iteration.