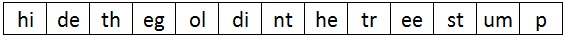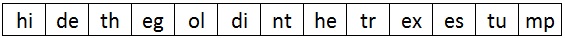Playfair Cipher
The Playfair Cipher was first described by Charles Wheatstone in 1854, and it was the first example of a Digraph Substitution Cipher. It is named after Lord Playfair, who heavily promoted the use of the cipher to the military.
When it was first put to the British Foreign Office as a cipher, it was rejected due to its perceived complexity. However, it was later adopted as a military cipher due to it being reasonably fast to use, and it requires no special equipment, whilst also providing a stronger cipher than a Monoalphabetic Substitution Cipher. It was used in the Second Boer War, and both World War I and World War II to different degrees. It is no longer used by military forces since the advent of powerful computers, but in its day it provided a relatively secure cipher which was easy to implement quite quickly.
Encryption
In order to encrypt using the Playfair Cipher, we must first draw up a Polybius Square (but without the need for the number headings). This is usually done using a keyword, and either combining "i" and "j" or omitting "q" from the square.
In order to encrypt using the Playfair Cipher, we must first draw up a Polybius Square (but without the need for the number headings). This is usually done using a keyword, and either combining "i" and "j" or omitting "q" from the square.
We must now split the plaintext up into digraphs (that is pairs of letters). On each digraph we peform the following encryption steps:
- If the digraph consists of the same letter twice (or there is only one letter left by itself at the end of the plaintext) then insert the letter "X" between the same letters (or at the end), and then continue with the rest of the steps.
- If the two letters appear on the same row in the square, then replace each letter by the letter immediately to the right of it in the square (cycling round to the left hand side if necessary).
- If the two letters appear in the same column in the square, then replace each letter by the letter immediately below it in the square (cycling round to the top of the square if necessary).
- Otherwise, form the rectangle for which the two plaintext letters are two opposit corners. Then replace each plaintext letter with the letter that forms the other corner of the rectangle that lies on the same row as that plaintext letter (being careful to maintain the order).
|
As an example we shall encrypt the plaintext "hide the gold in the tree stump" using the keyphrase playfair example. Firstly we must generate the Polybius Square that we are going to use. We do this by setting out a 5x5 grid, and filling it with the alphabet, starting with the letters of the keyphrase, and ignoring any letters we already have in the square. We are also going to combine "I" and "J" in the square.
|
The Mixed Square created for the Playfair Cipher, using the keyphrase playfair example.
|
We must now split the plaintext into digraphs. At this point it is a good idea to apply Rule 1, and split up any double letter digraphs by inserting an "x" between them. The first image below shows the initial digraph split of the plaintext, and the second image displays how we split up the "ee" into "ex" and "es". In this case, when we insert this extra "x", we no longer need to have one at the end of the plaintext.
The intial split into digraphs.
The digraph split once we apply Rule 1, and remove any digraphs made from two of the same letter.
We now take each digraph in turn and apply rule 2, 3 or 4 as necessary. Each step is show below with a visual representation of what is done for each digraph.
We can now take each of the ciphertext digraphs that we produced and put them all together.
The ciphertext digraphs
We can now write out the ciphertext as a long string "BMODZBXDNABEKUDMUIXMMOUVIF" or split it into block of 5 "BMODZ BXDNA BEKUD MUIXM MOUVI F" or even give it the same layout as the original "BMOD ZBX DNAB EK UDM UIXMM OUVIF"
Decryption
Decryption is nearly identical to the encryption process, except for rules 2 and 3 we must take the letters to the left and above respectively. Also, we remove any extra "X" in the decrypted text to reveal the final plaintext.
Decryption is nearly identical to the encryption process, except for rules 2 and 3 we must take the letters to the left and above respectively. Also, we remove any extra "X" in the decrypted text to reveal the final plaintext.
|
We shall decipher the ciphertext "UA ARBED EXAPO PR QNX AXANR" which has been encrypted using the keyword example. Firstly we must generate the Polybius Square which we are using, as shown to the right.
|
The Mixed Square with keyword example
|
The next step is to split the ciphertext into digraphs. There is no need to add any "X" in the decryption process as these will be revealed as we decrypt.
The ciphertext split into digraphs.
Now we apply the rules as needed to each digraph in the ciphertext.
We now combine all the digraphs together.
The plaintext digraphs.
So we get the message "we wilxl mexet at thex exit". When we remove the unnecessary "x"s we get a final plaintext of "we will meet at the exit". Note that we cannot just remove all the "x"s as one is part of the word "exit".
Discussion
The Playfair Cipher was an ingenious new way to encipher messages. It was the first of its kind, and opened up the world of cryptography to a whole new type of cipher: the polygraphic cipher. Although not secure in terms of modern cryptography, it was a substantial improvement over Monoalphabetic Substitution Ciphers, and significantly easier to use in the field than Polyalphabetic Substitution Ciphers.
The Playfair Cipher was an ingenious new way to encipher messages. It was the first of its kind, and opened up the world of cryptography to a whole new type of cipher: the polygraphic cipher. Although not secure in terms of modern cryptography, it was a substantial improvement over Monoalphabetic Substitution Ciphers, and significantly easier to use in the field than Polyalphabetic Substitution Ciphers.
We can see in the decryption example above that there are three digraphs the same in the ciphertext, namely "XA", and we also see that all three decrypt to the same plaintext "ex". This shows us that Digraph Substitution Ciphers are still susceptible to Frequency Analysis, but it has to be done on pairs of letters.
Because it is done on pairs of letters, this Frequency Analysis is significantly harder to crack. Firstly, for a monoalphabetic cipher we have 26 possible letters to check. For a general Digraph Cipher we have 26 x 26 = 676 possible pairings we need to check in our frequency analysis. In the instance of the Playfair Cipher, we cannot encrypt to a double letter, so we remove the 26 possibilities of double letters, giving us 650 possible digraphs we need to check. By hand this task in monumental, but with the help of a computer, it can be done in a matter of seconds.
Another useful weakness of the Playfair Cipher that can be exploited in cryptanalysis is the fact that the same pair of letters reversed will produce the same pair of letters reversed. For example, if the plaintext "er" encrypts to "HY", then the plaintext "re" will encrypt rto "YH". This is useful in some words in english such as "departed" which start and end with the same pair of letter in reverse.