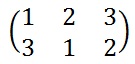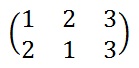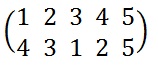Permutation Cipher
The Permutation Cipher is another form of Transposition Cipher. It is similar to Columnar Transposition in some ways, in that the columns are written in the same way, including how the keyword is used. However, the Permutation Cipher acts on blocks of letters (the lengths of the keyword), rather than the whole ciphertext.
|
Mathematically, a permutation is a rule that tells you how to rearrange a set of elements. For example, the permutation shown to the left (this is how we write a permutation mathematically), tells us that the first element is moved to the third position, the second element is moved to the first position and the third element is moved to the second position.
|
A simple permutation
|
If our set was the {Monday, Tuesday, Wednesday}, then after the permutation is applied we get {Tuesday,Wednesday,Monday}.
For sets bigger than the permutation, we apply the permutation to the smaller bits. For example, {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday} becomes {Tuesday, Wednesday, Monday, Friday, Saturday, Thursday} since we apply the permutation to the first 3 elements (as above), then to the second 3 elements, and join the results.
The Permutation Cipher works like this, acting on each block and reordering within the blocks.
Encryption
We choose a keyword, and split the plaintext into blocks that are the same length as the keyword. We write this in columns beneath the keyword. We then label each keyword letter in alphabetical order (if there are duplicates we take them in order of appearance). So far this is identical to Columnar Transposition. Now we reorder the columns, so that the numbers are in order (the letters of the keyword are in alphabetical order). We now read across the rows.
We choose a keyword, and split the plaintext into blocks that are the same length as the keyword. We write this in columns beneath the keyword. We then label each keyword letter in alphabetical order (if there are duplicates we take them in order of appearance). So far this is identical to Columnar Transposition. Now we reorder the columns, so that the numbers are in order (the letters of the keyword are in alphabetical order). We now read across the rows.
As an example we shall encrypt the plaintext "the quick brown fox jumped over the lazy dog" using the keyword bad.
|
We start by creating a grid that has 3 columns (as the keyword has 3 letters). In this grid we write out the plaintext beneath the keyword. We add a row with the numbers representing the alphabetical order of the letters of the keyword.
We then reorder the columns so that the numbers are in order, like in the image to the far right.
|
The grid filled with the plaintex, under the keyword bad, which has been labelled
|
The grid once the columns have been reordered so that the keyword is in alphabetical order
|
We then read off the ciphertext row by row to get "HTE UQI KCB ORW FNO JXU PME ODV RET EHL ZAY ODG" (the spaces are included for clarity, and would not be included in the final ciphertext).
|
Mathematically, the permutation that has been applied is shown to the right.
|
The mathematical permutation that has been applied.
|
Decryption
To decrypt a ciphertext encoded with the Permutation Cipher, we have to write out the ciphertext in columns (the same number as the length of the keyword). We then order the keyword alphabetically, and write the ordered keyword at the top of the columns. We then rearrange the columns to reform the keyword, and read of the plaintext in rows.
To decrypt a ciphertext encoded with the Permutation Cipher, we have to write out the ciphertext in columns (the same number as the length of the keyword). We then order the keyword alphabetically, and write the ordered keyword at the top of the columns. We then rearrange the columns to reform the keyword, and read of the plaintext in rows.
As an example, we shall decipher the ciphertext "QETHU BKICR FNOWO MUXJP VOEDE EHRTL DYAZO XXGXX" with keyword great.
|
We start by writing a grid with 5 columns (the length of the keyword), and filling it with the ciphertext, row by row. We label these with the numbers 1-5, and rearrange the keyword into alphabetical order before adding this to the top (AEGRT).
|
The grid with the ciphertext written in, and labelled with the keyword in alphabetical order.
|
The reordered grid, so that the keyword is formed.
|
We now reorder the letters of the keyword to form the actual keyword, and at the same time, reorder the columns in the same way.
|
The plaintext is now read off in rows to retrieve the same plaintext "the quick brown fox jumped over the lazy dog" (ignoring the nulls at the end).
|
The mathematical decryption permutationis shown to the right.
|
The decryption permutation.
|
|
Notice that this is not the same as the encryption permutation (shown to the right). To change from the encryption to the decryption (or vice versa), flip the two rows of the permutation, and reorder so the top row goes 1 2 3 ...
|
The encryption permutation
|
Discussion
In theory, all transposition ciphers are a type of permutation cipher, where the length of the key is the same as the length of the plaintext. In practice, this is a rather useless generalization, and it is almost always easier to find some other rule to describe the transposition than the rather cumbersome permutation that would be required.
In theory, all transposition ciphers are a type of permutation cipher, where the length of the key is the same as the length of the plaintext. In practice, this is a rather useless generalization, and it is almost always easier to find some other rule to describe the transposition than the rather cumbersome permutation that would be required.
We do not need a keyword to perform a Permutation Cipher, a permutation itself would do equally well (i.e. the numbers 1 to the chosen length in some mixed order). We use a keyword as it is easier to remember than a random string of numbers.
All of the things we discussed with Columnar Transposition are also the case here. We can use nulls to fill up the blank spaces if we want, but we don't have to. As we read across rows, using nulls is a real clue to the length of the keyword.
We can also perform the permutation a number of times. Some permutations, when done twice, will return the plaintext. This is clear when you reverse the permutation, as you get the same permutation as you started with.
The way to break a permutation cipher is to try out different permutations until you find a first block that makes sense. Once you have worked out the permutation, you can then use this to decrypt the rest of the intercept easily.