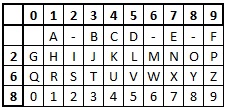
Straddling Checkerboard
The straddling checkerboard is another method of fractionating text. Unlike in the Polybius Square, where every character is represented by a pair of digits, in the straddling checkerboard a selection of letters (usually the most common) are represented by a single digit, and the rest are changed for two digits.
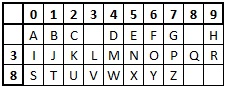
We set up the straddling checkerboard so that the first row of the board has the ten digits 0-9, then the alphabet is filled in to the grid beneath this, leaving two blanks in the first row of the alphabet. The numbers of these two columns label the second and third rows of the alphabet.
The standard checkerboard, with the alphabet in order, and the blanks at 3 and 8.
The order of the alphabet within the checkerboard is the main part of the key (the other part being which two numbers are selected), and we can generate this order in the same way as the Mixed Alphabet Cipher, using a keyword. It is usual, however, to populate the first row of letters with the high frequency letters (mnemonic ESTONIAR).
You should also note that, since there are 30 squares in our checkerboard, with two intentionally left blank in the top row, and 26 used for the letters, there are two remaining usable squares. One of these is usually filled with # as a numeric escape character (identifying that the following numeral is an actual number, not part of the ciphertext). The other could be used for a space, a full stop, or other punctuation mark.
Checkerboard with high frequency letters in the top row, and extra characters to fill the grid.
It is really important for the mechanics of the cipher to work that the two numbers that are used to labe rows 3 and 4 are not given a letter in the top row.
Encryption
To encrypt a message using the Straddling Checkerboard, we must first come up with the checkerboard itself, using a key to generate the alphabet to put in, and deciding on what will fill the extra boxes in the board. We must also choose which numbers will go down the side (and this forms part of our key).
To encrypt a message using the Straddling Checkerboard, we must first come up with the checkerboard itself, using a key to generate the alphabet to put in, and deciding on what will fill the extra boxes in the board. We must also choose which numbers will go down the side (and this forms part of our key).
With the checkerboard generated, we find each plaintext letter in the board. If it is in the top row of letters, it gets replaced by the single digit at the top of its column. If it is in one of the other rows, we use the number labelling the row first, then the column number.
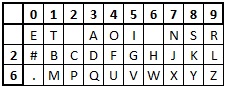
As an example we shall use the checkerboard given with the high frequency letters in the top row, the rest of the alphabet ordered by the keyphrase for the king (including a space and numeric escape), and the key numbers being 1 and 7. We shall encrypt the plaintext "attack at dawn".
First we need to generate the checkerboard, as below.
The checkerboard with high frequency letters, followed by the alphabet ordered by keyphrase "for the king". Includes a space and numeric escape character.
With this, we then look up each letter in the plaintext. The "a" is in the top row, so is only represented by a single digit "3". Similarly for the next few letters, but the "c" is in the second row, so we need the two digits "16" to represent it. Continuing in this way we get the numbers below.
The individual substitutions for the letters of the plaintext.
So our final ciphertext reads "32231 61311 32111 73756".
If we now consider a plaintext with a number in it, "attack at 6am", then we can see how the numeric escape key works. For this plaintext, we must insert a # before the "6" before encryption. Using the same checkerboard, we get the substitutions below.
The individual substitutions including a numeric escape character.
So the final ciphertext this time would be "32231 61311 32117 96370"
Decryption
To decrypt a ciphertext using the Straddling Checkerboard, we must again generate the checkerboard itself first. With this generated, we look at the first digit in the ciphertext. If it is one of the two digits down the left hand side, then we choose this row, and take the next digit to find which column to look in to locate the plaintext letter. If it is NOT one of the two letters on the far left of the checkerboard, then we locate the column with that number at the top, and choose the plaintext letter in the top row in this column.
To decrypt a ciphertext using the Straddling Checkerboard, we must again generate the checkerboard itself first. With this generated, we look at the first digit in the ciphertext. If it is one of the two digits down the left hand side, then we choose this row, and take the next digit to find which column to look in to locate the plaintext letter. If it is NOT one of the two letters on the far left of the checkerboard, then we locate the column with that number at the top, and choose the plaintext letter in the top row in this column.
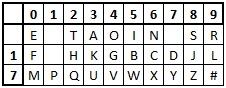
For our example, we shall use the checkerboard with high frequency letters in the top row, and then with the keyword decrypt# for the rest of the alphabet. We shall use 5 and 6 as the key numbers. We shall decypt the ciphertext "215055155250733750670506202660"
The checkerboard we get is shown below.
The checkerboard generated for this example
We start with the first digit in the ciphertext "2", which is NOT one of the key numbers, so we take the plaintext letter in the top row which is "a".
The next ciphertext digit is "1" which is again not a key number, so we get "t".
We now get "5" which is a key number, so we take the following digit as well to get "50", which is the plaintext reference for the space. So far we have "at ".
We get another "5", so take the pair "55", which gives us the numeric escape character. This tells us that the next digit is not a reference to the checkerboard, but rather part of the plaintext itself, so our plaintext becomes "at 1".
If we continue to break up the ciphertext in this way we get the table shown.
The final plaintext substitutions
This gives us the final plaintext "at 12 noon we leave".
Discussion
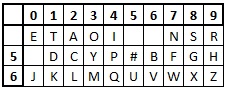
The first alteration to the Straddling Checkerboard that we can make is to have an extra row on the board. This time we would have 4 rows of letters, with 10 spaces each, but three spaces in the top row cannot be used, so we need an alphabet of 37 characters. Using the digits 0-9 and a space would get our alphabet up to this. Using this, we might get a checkerboard like below. In this case, we don't need a numeric escape character, since the digits are in the board itself.
The first alteration to the Straddling Checkerboard that we can make is to have an extra row on the board. This time we would have 4 rows of letters, with 10 spaces each, but three spaces in the top row cannot be used, so we need an alphabet of 37 characters. Using the digits 0-9 and a space would get our alphabet up to this. Using this, we might get a checkerboard like below. In this case, we don't need a numeric escape character, since the digits are in the board itself.
A bigger checkerboard, with space for the digits.
The Straddling Checkerboard is very good at fractionating text, but provides an element of compression when compared with the Polybius Square. This is due to the fact that the letters in the top row of the checkerboard are represented by only a single digit. If this row is populated with the high frequency characters, then the overall length of the ciphertext will be significantly decreased compared to the Polybius Square which would have two digits for these characters.
In terms of cryptanalysis, the fact that some letters are enciphered to single digits, whilst others are encrypted to pairs of digits, means that the cryptanalysist has to work out which are the single digits. By choosing the wrong ones, he can head down a very wrong path, making this slightly more secure than the Polybius Square (as it is less susceptible to frequency analysis).